Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian đội I làm một mình xong công việc là x (ngày) (x > 4)
Nếu họ làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 6 ngày
⇒ thời gian một mình đội II làm xong công việc là x + 6 (ngày).
Mỗi ngày, đội I làm được: 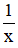
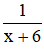
⇒ Một ngày cả hai đội cùng làm được: 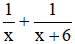
Cả hai đội cùng làm thì trong 4 ngày xong việc nên ta có phương trình:
⇔ 4.(2x + 6) = x(x + 6)
⇔ 8x + 24 = x2 + 6x
⇔ x2 – 2x – 24 = 0
Có a = 1; b = -2; c = -24 ⇒ Δ’ = (-1)2 – 1.(-24) = 25 > 0
Phương trình có hai nghiệm
Trong hai nghiệm chỉ có nghiệm x = 6 thỏa mãn điều kiện.
Vậy:
Một mình đội I làm trong 6 ngày thì xong việc.
Một mình đội II làm trong 12 ngày thì xong việc.

- Giả sử nếu làm riêng thì tổ 1 hoàn thàn công việc trong x giờ => tổ 2 làm trong x + 3 giờ (do tổ 1 hoàn thành sớm hơn tổ 2 là 3 giờ mà)
- Do tổ 1 làm riêng thì hoàn thành cv trong x giờ nên mỗi giờ làm được 1/x công việc.
- Tương tự, tổ 2 mỗi giờ làm được 1/(x+3) công việc.
- Nếu hai tổ củng làm thì mỗi giờ hoàn thành 1/x + 1/(x+2) công việc.
- Mặt khác, do cả hai tổ cùng là trong 2 giờ thì xong công việc nên mỗi giờ làm được 1/2 công việc.
Vậy ta có: 1/x + 1/(x+3) = 1/2 (quy đồng, nhân chéo rồi ra phương trình bậc 2, tự làm nhé)
=> x = 3.
Vậy nếu làm riêng tổ 1 hoàn thành công việc trong 3h, tổ 2 hoàn thành trong 6h
thử lại: 1/3 + 1/6 = 1/2

Gọi thời gian làm riêng của người thứ nhất là x
Thời gian làm riêng của người thứ hai là x+3
Theo đề, ta có: 1/x+1/(x+3)=1/2
=>2x+6+2x=x(x+3)
=>x2+3x=4x+6
=>x2-x-6=0
=>x=3
Vậy: Thời gian làm riêng của người 1 và người 2 lần lượt là 3h và 6h

Gọi thời gian đội I, đội II làm một mình xong công việc lần lượt là x, y (đơn vị ngày, đk :x, y > 4)
+ Thì mỗi ngày đội I làm được 1/x (công việc), đội II được 1/y (công việc)
Vì hai đội cùng làm thì 4 ngày xong nên mỗi ngày hai đội làm được 1/4 (công việc), nên ta có phương trình 1/x + 1/y =1/4.
+ Phần công việc đội I làm trong 3 ngày là 3/x (công việc), phần công việc đội II làm trong 6 ngày là 6/y. Vì khi đội I làm 3 ngày, đội II làm 6 ngày thì xong công việc nên ta có pt : 3/x + 6/y = 1
ta có hpt :1/x + 1/y =1/4 và 3/x + 6/y = 1
=> x=6 , y=12
k mk nha!!

Gọi thời gian tổ I hoàn thành là xx(h), khi đó thời gian tổ 2 hoàn thành là x+3x+3(h)
Khi đó, trong 1h thì tổ I và tổ II lần lượt làm đc là 1x1x(phần công việc) và 1x+31x+3 (phần công việc)
Do đó, trong 1h thì 2 tổ làm đc số phần công việc là 1x+1x+31x+1x+3(phần công việc)
Lại có 2 tổ làm chung thì hoàn thành công việc trong 2h, do đó trong 1h cả hai tổ làm đc 1212 (phần công việc). Do đó
1x+1x+3=121x+1x+3=12
⇒2(x+3)+2x=x(x+3)⇒2(x+3)+2x=x(x+3)
⇔x2−x−6=0⇔x2−x−6=0
⇔(x−3)(x+2)=0⇔(x−3)(x+2)=0
Vậy x=3x=3 hoặc x=−2x=−2(loại)
Suy ra x+3=6x+3=6
Vậy tổ I và tổ II làm trong 33(h) và trong 66(h) thì xong.
Viết nhầm: Câu cuối phải là: Vậy tổ 1 và tổ 2 làm trong 3 và 6 giờ thì xong

* Giả sử nếu làm riêng thì tổ 1 hoàn thàn công việc trong x giờ => tổ 2 làm trong x + 3 giờ (do tổ 1 hoàn thành sớm hơn tổ 2 là 3 giờ mà)
* Do tổ 1 làm riêng thì hoàn thành cv trong x giờ nên mỗi giờ làm được 1/x công việc.
* Tương tự, tổ 2 mỗi giờ làm được \(\frac{1}{x+3}\) công việc.
* Nếu hai tổ củng làm thì mỗi giờ hoàn thành \(\frac{1}{x}\) + \(\frac{1}{x+2}\) công việc.
* Mặt khác, do cả hai tổ cùng là trong 2 giờ thì xong công việc nên mỗi giờ làm được \(\frac{1}{2}\)công việc.
Vậy ta có: \(\frac{1}{x}\) + \(\frac{1}{x+3}\) = \(\frac{1}{2}\) (quy đồng, nhân chéo rồi ra phương trình bậc 2, bạn tự làm nhé!!!)
=> x = 3.
Vậy nếu làm riêng tổ 1 hoàn thành công việc trong 3h, tổ 2 hoàn thành trong 6h
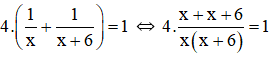
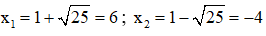
fgshj