Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn (C) tiếp xúc với d1 và d2 , suy ra tâm của nó nằm trên đường phân giác của góc (d1;d2)
Khoảng cách từ một điểm bất kì trên phân giác của góc đến hai cạnh của góc thì bằng nhau, ta có:
\(\frac{\left|3x-4y+1\right|}{5}=\frac{\left|6x+8y-1\right|}{10}\Leftrightarrow\orbr{\begin{cases}2\left(3x-4y+1\right)=6x+8y-1\\2\left(3x-4y+1\right)=-6x-8y+1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}16y-3=0\\12x+1=0\end{cases}}\)
Xét hệ \(\hept{\begin{cases}3x+y-1=0\\16y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{13}{48}\\y=\frac{3}{16}\end{cases}}\Rightarrow I_1\left(\frac{13}{48};\frac{3}{16}\right)\Rightarrow R_1=\frac{17}{80}\)
\(\Rightarrow\left(C_1\right):\left(x-\frac{13}{48}\right)^2+\left(y-\frac{3}{16}\right)^2=\frac{289}{6400}\)
Xét hệ: \(\hept{\begin{cases}3x+y-1=0\\12x+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-\frac{1}{12}\\y=\frac{5}{4}\end{cases}}}\Rightarrow I_2\left(-\frac{1}{12};\frac{5}{4}\right)\Rightarrow R_2=\frac{17}{20}\)
\(\Rightarrow\left(C_2\right):\left(x+\frac{1}{12}\right)^2+\left(y-\frac{5}{4}\right)^2=\frac{289}{400}\).
Đường tròn (C) tiếp xúc với d1 và d2 , suy ra tâm của nó nằm trên đường phân giác của góc (d1;d2)
Khoảng cách từ một điểm bất kì trên phân giác của góc đến hai cạnh của góc thì bằng nhau, ta có:
|3x−4y+1|5 =|6x+8y−1|10 ⇔[
| 2(3x−4y+1)=6x+8y−1 |
| 2(3x−4y+1)=−6x−8y+1 |
⇔[
| 16y−3=0 |
| 12x+1=0 |
Xét hệ {
| 3x+y−1=0 |
| 16y−3=0 |
⇔{
| x=1348 |
| y=316 |
⇒I1(1348 ;316 )⇒R1=1780
⇒(C1):(x−1348 )2+(y−316 )2=2896400
Xét hệ: {
| 3x+y−1=0 |
| 12x+1=0 |
⇔{
| x=−112 |
| y=54 |
⇒I2(−112 ;54 )⇒R2=1720
⇒(C2):(x+112 )2+(y−54 )2=289400 .

Giả sử đường tròn cần lập có tâm O; bán kính R.
Đường thẳng Δ đi qua M(2; -2) và có VTPT là n→(4; 3) nên đường thẳng này có 1 VTCP là u→(3; -4) . Phương trình tham số của đường thẳng Δ là:
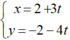
O nằm trên Δ ⇒ O(2 + 3t; -2 – 4t)
Đường tròn (O; R) tiếp xúc với d1 và d2 ⇒ d(O; d1) = d(O; d2) = R
Ta có: d(O; d1) = d(O; d2)
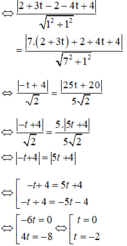
+ Với t = 0 ⇒ O(2; -2) ⇒ R = d(O; d1) = 2√2
Phương trình đường tròn: (x – 2)2 + (y + 2)2 = 8.
+ Với t = -2 ⇒ O(-4; 6) , R = d(O; d1) = 3√2
Phương trình đường tròn: (x + 4)2 + (y – 6)2 = 18
Vậy có hai phương trình đường tròn thỏa mãn là:
(x – 2)2 + (y + 2)2 = 8 hoặc (x + 4)2 + (y – 6)2 = 18

Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)

a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:
$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$
Với I là tâm đường tròn, A là điểm trên đường tròn.
Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$
Thay vào công thức ta được:
$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$
Vậy bán kính của đường tròn là $\sqrt{34}$.
Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:
$(x-2)^2 + (y-3)^2 = 34$
b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.
Ta có phương trình đường tròn chính giữa:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Tại điểm M(x,y) trên đường tròn, ta có:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:
$y - y_M = y'(x-x_M)$
Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:
$y + 5 = \frac{-(x-1)}{y+5}(x-1)$
Simplifying:
$x(y+5) + y(x-1) = 6$
Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến

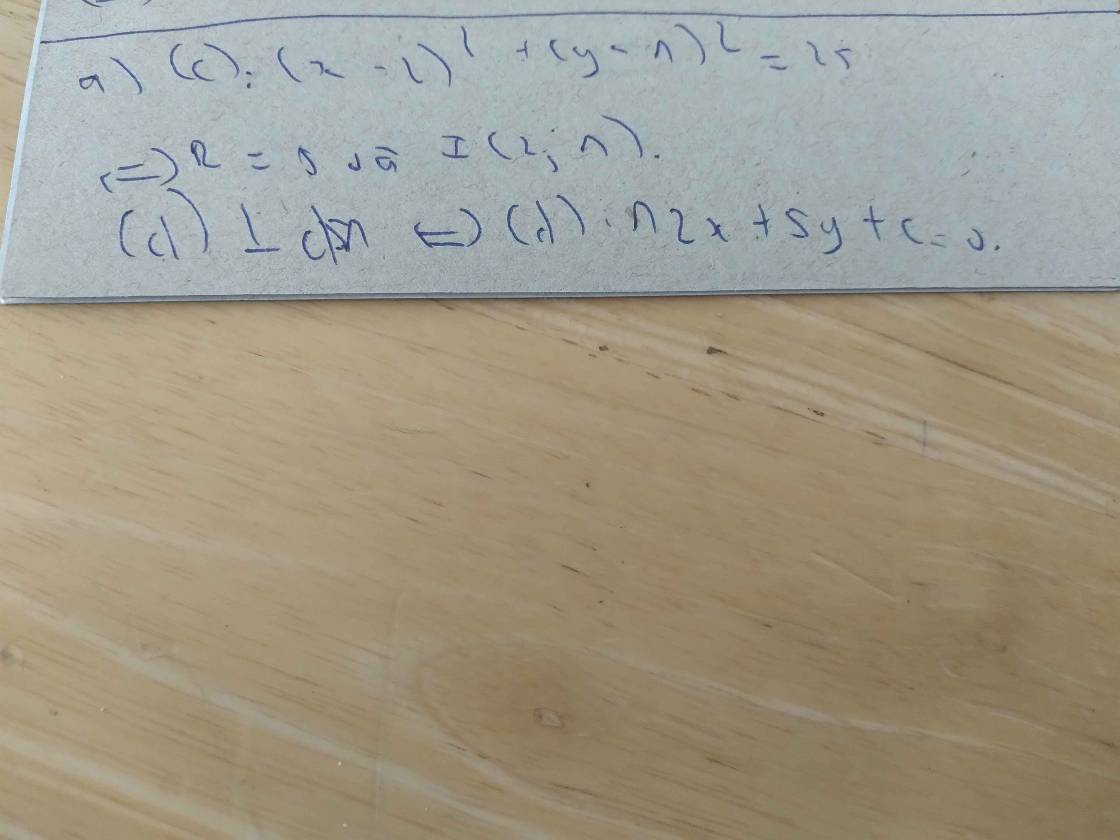

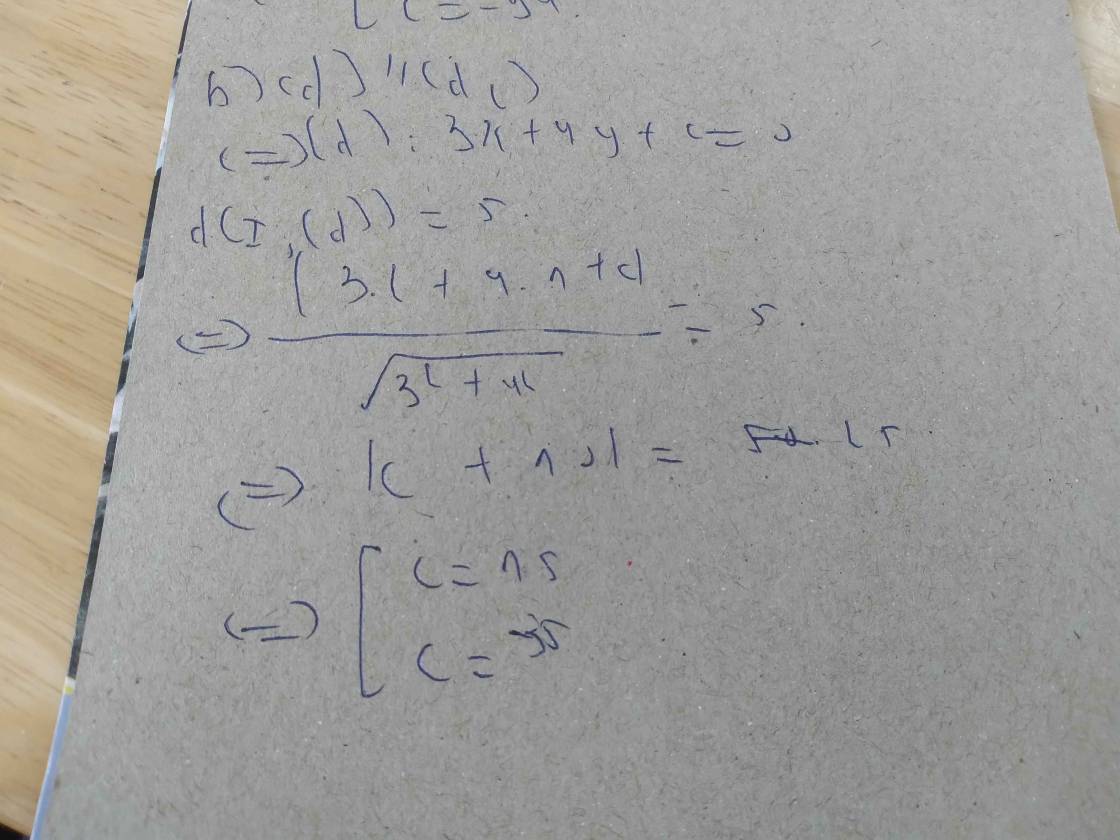
Gọi đường tròn tâm \(I\left(a;b\right)\Rightarrow d\left(I;d_1\right)=d\left(I;d_2\right)\)
\(\Rightarrow\dfrac{\left|3a-4b+1\right|}{5}=\dfrac{\left|4a+3b-7\right|}{5}\)
\(\Rightarrow\left[{}\begin{matrix}3a-4b+1=4a+3b-7\\3a-4b+1=-4a-3b+7\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=-7b+8\\b=7a-6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(-7b+8;b\right)\\I\left(a;7a-6\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}IA^2=\left(-7b+6\right)^2+\left(b-3\right)^2\\IA^2=\left(a-2\right)^2+\left(7a-9\right)^2\end{matrix}\right.\)
\(IA^2=d^2\left(I;d_1\right)\Rightarrow\left[{}\begin{matrix}\left(-7b+6\right)^2+\left(b-3\right)^2=\left(b-1\right)^2\\\left(a-2\right)^2+\left(7a-9\right)^2=\left(a-1\right)^2\end{matrix}\right.\)
Giờ giải pt bậc 2 là được
Anh ơi! Khi kết hợp phương trình mà giải ra vô nghiệm thì tại sao lại là phân giác ngoài của góc tạo bởi 2 đường thẳng vậy ạ anh