Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có ![]() đây là 1 VTCP của đường thẳng đã cho.
đây là 1 VTCP của đường thẳng đã cho.
Suy ra đường thẳng đã cho có 1 VTPT là ![]() ( 4; -2)
( 4; -2)
Lại có vecto ![]() cùng phương với VTPt trên nên vecto
cùng phương với VTPt trên nên vecto ![]() cũng là 1 VTPT của đường thẳng đã cho.
cũng là 1 VTPT của đường thẳng đã cho.
Chọn C.

Đáp án A
Từ giả thiết ta suy ra hai đường thẳng d và d’ đồng phẳng, do đó khẳng định A là sai.

Vectơ ![]() cũng là vectơ chỉ phương của đường thẳng đã cho.
cũng là vectơ chỉ phương của đường thẳng đã cho.
Khi đó đường thẳng d có phương trình tham số:
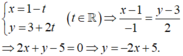
Chọn D

Chọn B.
Ta có:
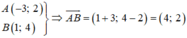
Vậy vectơ chỉ phương của đường thẳng đi qua hai điểm A(-3;2) và B(1;4) là 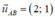

Khi phương trình đường thẳng cho dưới dạng tham số: 
Thì đường thẳng có VTCP là ![]() (a; b)
(a; b)
Do đó; phương trình đường thẳng đã cho có vecto chỉ phương là ![]() (6; 0)
(6; 0)
Lại có: vecto ![]() cùng phương với vecto
cùng phương với vecto ![]() nên vecto
nên vecto ![]() cũng là VTCP của đường thẳng đã cho.
cũng là VTCP của đường thẳng đã cho.
Chọn D.

Đáp án A
Trục Ox có phương trình tổng quát là: y= 0.
Đường thẳng này có VTPT là ( 0; 1) và VTCP là (1; 0)
Các đường thẳng song song với trục Ox sẽ có cùng VTPT và có cùng VTCP với trục Ox. Nên đường thẳng song song với trục Ox có VTCP là (1; 0) .

Đáp án A
Trục Ox có phương trình là y= 0.
Nên đường thẳng này có 1 VTPT là: n → ( 0 ; 1 )
Do đó 1 VTCP của đường thẳng là (1; 0)

Đáp án B
Trục Oy có phương trình là x = 0.
Nên đường thẳng này có 1 VTPT là n → ( 1 ; 0 )
Do đó:1 VTCP của đường thẳng là (0; 1)
Mà 2 vectơ (0; 1) và (0; -1) là 2 vectơ cùng phương nên vectơ (0; -1) cũng là VTCP đối với trục Oy.
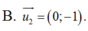
Ta có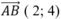 là 1 VTCP của đường thẳng đã cho.
là 1 VTCP của đường thẳng đã cho.
Chọn A.