Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(BC=2AM=2\times5=10cm\)
ta có \(MH=\sqrt{AM^2-AH^2}=\sqrt{5^2-4^2}=3cm\)
nên \(HB=MB-MH=5-4=1cm\) mà ta có \(AB^2=BH.BC=1.10\Rightarrow AB=\sqrt{10}\Rightarrow AC=\sqrt{BC^2-AB^2}=3\sqrt{10}\left(cm\right)\)

độ dài cạnh huyền là:
5x2=10(cm)
độ dài cạnh góc vuông thứ hai là:
\(\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
độ dài đường cao là:
\(5\cdot5\sqrt{3}:10=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)

câu 2
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5

Giả sử tam giác ABC có góc (BAC) = 90 ° , AH ⊥ BC, BC = 5, AH = 2 và BH < CH
Ta có: BH + CH = 5 (1)
Theo hệ thức liên hệ giữa đường cao và cạnh huyền trong tam giác, ta có:
BH.CH = A H 2 = 2 2 = 4 (2)
Từ (1) và (2) suy ra: BH = 1 và CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A B 2 = BH.BC = 1.5 = 5
Suy ra: AB = 5

Goi 2 canh goc vuong la b va c (b > c)
Ap dung he thuc luong va dinh ly Pythagore ta co he pt :
{ b.c = 5.2 = 10 (1)
{ b^2 + c^2 = 5^2 = 25 (2)
(1) ---> 2bc = 20 (3)
(2) + (3) ---> (b+c)^2 = 45 ---> b+c = 3 can 5 (4)
(2) - (3) ---> (b-c)^2 = 5 ---> b-c = can 5 (5)
(4),(5) ---> b = 2 can 5 ; c = can 5
Vay canh nho nhat cua tam giac vuong do la can 5.

Mình làm thế này có ổn ko?
Gọi tam giác ABC vuông tại A cạnh huyền BC là 10cm và đường cao AH (H thuộc BC) là 6cm
Vậy ta có: \(HB+HC=10\)
Dùng hệ thức lượng trong tam giác vuông ta có: \(HB.HC=AH^2=36\)
Vậy ta có: \(\hept{\begin{cases}HB+HC=10=S\\HB.HC=36=P\end{cases}}\)\
Vì \(S^2-4P=10^2-4.36\)\(=100-144=-44< 0\)
Vậy không có HB, HC nào thỏa mãn hpt trên (trái với hệ thức lượng trong tam giác vuông)
Vậy không có tam giác vuông có cạnh huyền là 10cm và đường cao tương ứng với cạnh huyền là 6cm

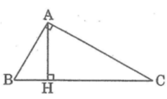

*cách vẽ:
- Vẽ đoạn thẳng BC = 4cm
-Vẽ nửa đường tròn đường kính BC
-Vẽ đường thẳng xy nằm trên nửa mặt phẳng chứa nửa đường tròn đường kính BC và xy // BC ,cách BC một khoảng bằng 1,5cm
- Đường thẳng xy cắt nửa đường tròn đường kính BC tại A và A’.Nối AB, AC, A’B, A’C ta được tam giác ABC cần vẽ
*Chứng minh:
Vì xy cách BC một khoảng bằng 1,5cm nhỏ hơn BC/2 = 2cm nên xy cắt nửa đường tròn đường kính BC
Ta lại có tam giác ABC nội tiếp trong nửa đường tròn đường kính BC nên
góc (BAC) = 90 °
Mặt khác AH ⊥ BC và AH =1,5cm.