Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

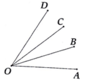
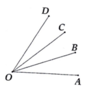
a) Ta có A O B ^ < A O C ^ nên tia OB nằm giữa hai tia OA và OC. Theo tính chất cộng góc, suy ra 20°, nên A O B ^ = B O C ^ . Vậy OB là tia phân giác của góc AOC.
b) Tương tự ý a), tính được
C O D ^ = 20° và B O D ^ = 40°.
c) Ta có B O C ^ = C O D ^ = B O D ^ 2 (cùng bằng 20°). Do đó, tia OC là tia phân giác của góc BOD.

a/ Vì tia OB là tia phân giác của góc AOC nên tia OB nên ta có :
\(\widehat{AOB}:\frac{1}{2}=\widehat{AOC}\)
\(60^0:\frac{1}{2}=120^0\)
b/ Vì hai góc COD và AOB là hai góc kề bù nên ta có tổng số đo là\(180^0\). Ta có :
\(\widehat{COD}+\widehat{AOC}=\widehat{DOA}\)
\(\widehat{COD}+120^0=180^0\)
\(\widehat{COD}=180^0-120^0\)
\(\widehat{COD}=60^0\)
ĐS:\(\widehat{AOC}=120^0\)
\(\widehat{COD}=60^0\)
Tìm các chữ số a, b sao cho 2018ab đồng thời chia hết cho 5 và 13