Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

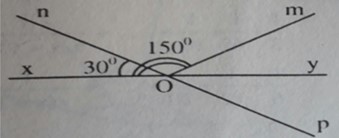
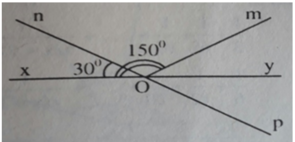
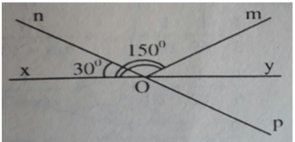
\(\widehat{XOM}\)= \(150^o\)
\(\widehat{XON}\) = \(30^o\)
Nên góc \(\widehat{MON}\) = \(\widehat{XOM}\) - \(\widehat{XON}\) = \(150^o\)- \(30^o\) = \(120^o\) Tia Oy là tia phân giác của góc \(\widehat{MOP}\)
VÌ tia Oy nằm giữa hai tia Om và Op , có chung một độ là \(30^o\) CHÚC BẠN THÀNH CÔNG
a. Ta có ; \(\widehat{mOn}=\widehat{xOm}-\widehat{xOn}\)
\(\Rightarrow\widehat{mOn}=150^o-30^o\)
\(\Rightarrow\widehat{mOn}=120^o\)
Vậy \(\widehat{mOn}=120^o\)
b . Ta có ; \(\widehat{yOm}=\widehat{xOy}-\widehat{xOm}\)
\(\Rightarrow\widehat{yOm}=180^o-150^o\)
\(\Rightarrow\widehat{yOm}=30^o\) \((1)\)
Mặt khác ; \(\widehat{yOp}=\widehat{xOn}\)\((\)đối đỉnh \()\)
mà bài cho \(\widehat{xOn}=30^o\)
\(\Rightarrow\widehat{yOp}=30^o\)\((2)\)
Từ \((1)\)và \((2)\)suy ra ;
\(\widehat{yOm}=\widehat{yOp}=30^o\)
\(\Rightarrow\)tia Oy là tia phân giác của \(\widehat{mOp}\)
Học tốt

a) Trên cùng nửa mặt phẳng bờ Ox có xOm = 30o ; xOt = 150o
=> xOm < xOt (30o < 150o)
=> Tia Om nằm giữa hai tia Ox và Ot
=> xOm + mOt = xOt (1)
Thay xOm = 30o ; xOt = 150o vào (1) ta có :
30o + mOt = 150o
=> mOt = 150o - 30o = 120o
b) Vì mOt và tOz là 2 góc kề bù
=> mOt + tOz = 180o (2)
Thay mOt = 120o vào (2) ta có :
120o + tOz = 180o
=> tOz = 180o - 120o = 60o
Vì xOt và tOy là 2 góc kề bù
=> xOt + tOy = 180o (3)
Thay xOt = 150o vào (3) ta có :
150o + tOy = 180o
=> tOy = 180o - 150o = 30o
Trên cùng nửa mặt phẳng bờ Ot có tOy = 30o ; tOz = 60o
=> tOy < tOz (30o < 60o)
=> Tia Oy nằm giữa hai tia Ot và Oz (4)
=> tOy + yOz = tOz (5)
Thay tOy = 30o ; tOz = 60o vào (5) ta có :
30o + yOz = 60o
=> yOz = 60o - 30o = 30o
Vì tOy = 30o và yOz = 30o => tOy = yOz (6)
Từ (4) và (6) => Tia Oy là tia phân giác của zOt
k nha bn !

1/ vì xot > xom
=> om nằm giữa ox và ot
vì thế: xom + mot = xot
=> mot = xot - xom = 150 = 30 = 120 độ
2/ vì xoy là góc bẹt nên = 180 độ
vì xoy > xot
=> ot nằm giữa ox ,oy
vì thế: xot + toy = xoy
=> toy = xoy - xot = 180 - 150 = 30 độ
theo đề: oz và om đối nhau tọa góc moz = góc bẹt = 180 độ
vì moz > mot
=> ot nằm giữa om ,oz
vì thế: mot + toz = moz
=> toz = moz - mot = 180 - 120 =60 độ
vì toz > toy
=> oy nằm giữa ot ,oz
vì thế: toy + yoz = toz
=> yoz = toz - toy = 60 - 30 = 30 độ
vì oy nằm giữa ot, oz
toy = yoz = 30 độ
=>Oy là tia phân giác của góc zOt
1/ vì xot > xom
=> om nằm giữa ox và ot
vì thế: xom + mot = xot
=> mot = xot - xom = 150 = 30 = 120 độ
2/ vì xoy là góc bẹt nên = 180 độ
vì xoy > xot
=> ot nằm giữa ox ,oy
vì thế: xot + toy = xoy
=> toy = xoy - xot = 180 - 150 = 30 độ
theo đề: oz và om đối nhau tọa góc moz = góc bẹt = 180 độ
vì moz > mot
=> ot nằm giữa om ,oz
vì thế: mot + toz = moz
=> toz = moz - mot = 180 - 120 =60 độ
vì toz > toy
=> oy nằm giữa ot ,oz
vì thế: toy + yoz = toz
=> yoz = toz - toy = 60 - 30 = 30 độ
vì oy nằm giữa ot, oz
toy = yoz = 30 độ
=>Oy là tia phân giác của góc zOt

a)Theo hình ta có:\(\widehat{xOm}+\widehat{mOt}=\widehat{xOt}\)
\(\Rightarrow30^0+\widehat{mOt}=150^0\)
\(\Rightarrow\widehat{mOt}=120^0\)
b)Ta có:\(\widehat{xOt}+\widehat{tOy}=180^0\)(góc bẹt)
\(\Rightarrow150^0+\widehat{tOy}=180^0\)
\(\Rightarrow\widehat{tOy}=30^0\)
Vì tia Oz là tia đối của tia Om\(\Rightarrow\widehat{xOm}=\widehat{yOz}=30^0\left(đđ\right)\)
Do đó \(\widehat{tOy}=\widehat{yOz}\). Hay Oy là tia p/giác của góc zOt

Giải:
1) Vì +) Om; Ot cùng ∈ 1 nửa mặt phẳng bờ xy
+) \(x\widehat{O}m< x\widehat{O}t\left(130^o< 150^o\right)\)
⇒Om nằm giữa Ox và Ot
\(\Rightarrow x\widehat{O}m+m\widehat{O}t=x\widehat{O}t\)
\(130^o+m\widehat{O}t=150^o\)
\(m\widehat{O}t=150^o-130^o\)
\(m\widehat{O}t=20^o\)
2) Vì \(x\widehat{O}y\) là góc bẹt
\(\Rightarrow x\widehat{O}y=180^o\)
\(\Rightarrow x\widehat{O}t+t\widehat{O}y=180^o\) (2 góc kề bù)
\(150^o+t\widehat{O}y=180^o\)
\(t\widehat{O}y=180^o-150^o\)
\(t\widehat{O}y=30^o\)
Vì \(x\widehat{O}t>t\widehat{O}y\left(150^o>30^o\right)\)
⇒Oy không phải là tia p/g của \(x\widehat{O}t\)