K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 9 2021
Độ dài cạnh góc vuông lớn là:
\(\sqrt{6.4\cdot10}=8\left(cm\right)\)
23 tháng 9 2021
Áp dụng HTL
\(AC^2=CH\cdot BC=6,4\left(6,4+3,6\right)=64\\ \Rightarrow AC=8\left(cm\right)\)
Vậy ...
N
21 tháng 11 2021
a. Vì \(\widehat{AMB}=90^0\) (góc nt chắn nửa đg tròn) nên AMB vuông tại M
Áp dụng HTL: \(BM.BC=AB^2=\left(2R\right)^2=4R^2\)
b. Vì AMBD nội tiếp (O) nên \(\widehat{MAB}=\widehat{HDB}\) (cùng chắn MB)
Vì \(\widehat{MAH}=\widehat{HDB};\widehat{MHA}=\widehat{BHD}=90^0\) nên \(\Delta MAH\sim\Delta BDH\left(g.g\right)\)
\(\Rightarrow\dfrac{HM}{HB}=\dfrac{HA}{HD}\Rightarrow MD.HD=HA.HB\)
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
11 tháng 4 2023
a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2
20 tháng 9 2021
Bài là tam giác vuông hả bạn?
Ta có : BC = BH + CH = \(\sqrt{2}+\sqrt{8}=3\sqrt{2}\)
Xét △ ABC vuông tại A, đường cao AH có:
\(AB^2\)=BH.BC ( hệ thức lượng trong tam giác vuông)
=> \(AB^2=\sqrt{2}.3\sqrt{2}=6\)
=> \(AB=\sqrt{6}\)
\(AC^2=BC.HC\)
=> \(AC^2=\sqrt{8}.3\sqrt{2}=12\)
=>\(AC=2\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\sqrt{6}.2\sqrt{6}=3\sqrt{2}\left(cm^2\right)\)
AN
1
2 tháng 3 2023
Bài 9:
a: Xét tứ giác OPMN có
góc OPM+góc ONM=180 độ
=>OPMN là tứ giác nội tiếp
b: \(MN=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH vuông góc AB
Xét tứ giác OHNM có
góc OHM=goc ONM=90 độ
=>OHNM là tứ giác nội tiép
=>góc MHN=góc MON
HK
0
12 tháng 10 2021
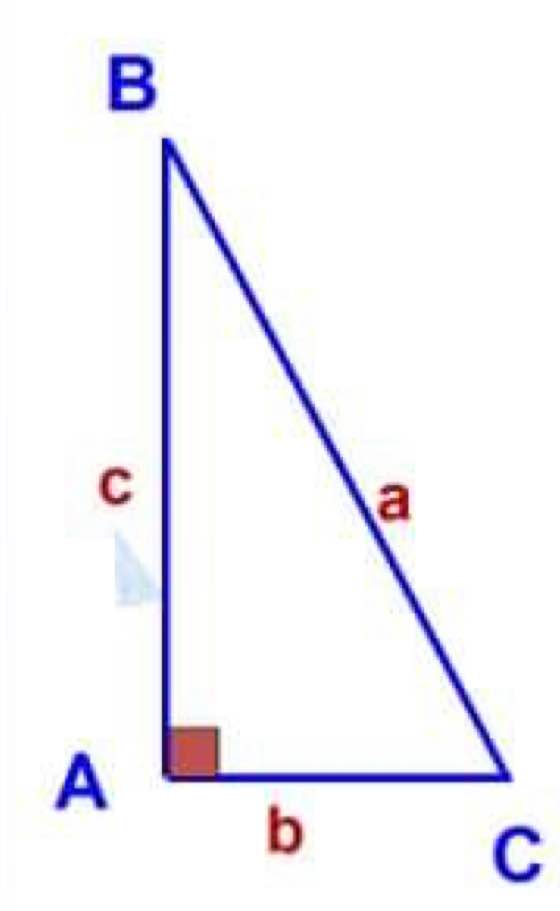
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)
Vì \(\widehat{BEC}=\widehat{BKC}=90^0\)(góc nt chắn nửa đg tròn) nên \(HK\perp MC;ME\perp HC\)
Xét tam giác HMC có 2 đường cao HK,ME (cm trên) cắt nhau tại B nên B là trực tâm
Do đó BC⊥MH