Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

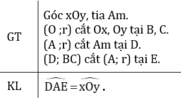
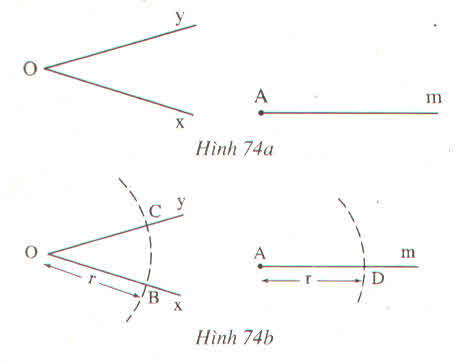
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
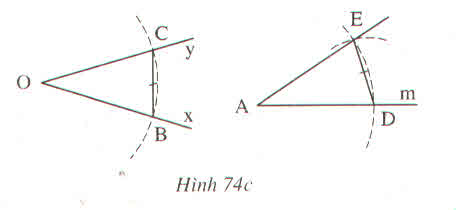
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
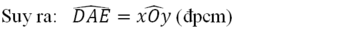

Xét tam giác OBC và tam giác AED có
OB = AE (GT)
OC = AD (GT)
BC = ED (GT)
=> tam giác OBC = tam giác AED
=> góc xOy = góc DAE (2 góc tương ứng)
Vậy góc xOy = góc DAE

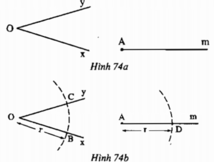
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra \(\widehat{DAE}\)=\(\widehat{BOC}\)(hai góc tương tứng)
vậy
\(\widehat{DAE}\)=\(\widehat{xOy}\).

Xét tam giác OBC và tam giác AED có:
OB = AE (GT)
OC = AD (GT)
BC = ED (GT)
=> tam giác OBC = tam giác AED (c.c.c)
=> \(\widehat{xOy}\)=\(\widehat{DAE}\) (đpcm)
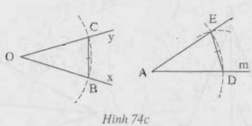
Xét tam giác DAE và tam giác BOC:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
nên tam giác DAE= tam giác BOC( HAI GÓC TƯƠNG ỨNG)
NÊN ..............