Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì dao động của vật T = 2π/ω = 0,5s
Xét thời gian 7/48s = 7T/14 = T/8 + T/6
Ta có hình vẽ
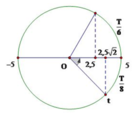
Từ hình vẽ ta thấy rằng, sau 7/48s vật đi qua vị trí có li độ x = 2,5 cm
Đáp án D

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
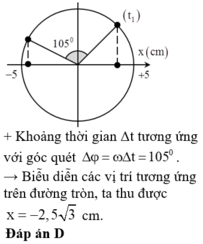
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

Mấy bài như này bạn chỉ cần tìm góc quay của nó rồi biểu diễn trên đường tròn là sẽ ra li độ
a/ \(\varphi=\omega t=4\pi.2,05=\dfrac{41}{5}\pi\left(rad\right)=\dfrac{\pi}{6}+8\pi+\dfrac{\pi}{30}\)
\(\Rightarrow x=-A\sin\left(\dfrac{\pi}{30}\right)=-1,045\left(cm\right)\)
b/ \(\varphi=\omega t=4\pi.1,15=\dfrac{23}{5}\pi\left(rad\right)=\dfrac{\pi}{3}+4\pi+\dfrac{4}{15}\pi\)
\(\Rightarrow x=A\cos\left(\dfrac{4}{15}\pi\right)=6,69\left(cm\right)\)

Chu kì \(T=\dfrac{2\pi}{\omega}=0,5s\)
Trong thời gian 7/48s thì véc tơ quay đã quay một góc là:
\(\alpha=\dfrac{\dfrac{7}{48}}{0,5}.360=26,25^0\)
Biểu diễn dao động bằng véc tơ quay, ban đầu qua li độ \(2,5\sqrt 2\) và đang giảm
ứng với vị trí M như hình vẽ
Lúc sau, véc tơ quay đến N, hình chiếu của N lên trục tọa độ sẽ cho biết li độ mới.
\(x=5.\cos(45-26,25)\approx4,73cm\)
@Thư Hoàngg: Bạn Quang Hưng nhầm trong việc tính góc α,
giá trị đúng phải là: \(\alpha = 105^0\), như vậy ban đầu véc tơ quay ở M quay 1050
sẽ đến N, khi đó ON tạo với Ox 1 góc là: 105 - 45 = 600
Suy ra: \(x=5.\cos(60^0)=2,5cm.\)
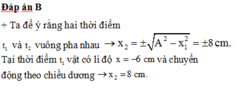
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,5s\)
a) t = 0,124s = T/4
Biểu diễn dao động bằng véc tơ quay, ta có:
Ban đầu, vị trí của vật ứng với véc tơ quay tại M, sau T/4, vị trí đó đến điểm N.
\(\Rightarrow x = 8\cos 30^0=4\sqrt 3(cm)\)
b) Hoàn toàn tương tự, ta tìm được li độ của vật sau 0,3125s là \(x=0cm\)