Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Số cách xếp 8 học sinh nói trên ngồi xung quanh một bạn tròn là 7 !.
+ Đếm số cách xếp 8 học sinh ngồi xung quanh một bàn tròn mà hai học sinh Hải và Liên ngồi cạnh nhau:
Trước tiên, số cách xếp 7 học sinh (trừ bạn Hải sẽ xếp sau) ngồi xung quanh một bàn tròn là 6 !
Khi đó có 2 cách xếp chỗ ngồi cho bạn Hải (ở bên trái hoặc bên phải bạn Liên).
Theo quy tắc nhân, sẽ có 6!.2 cách xếp 8 bạn ngồi xung quanh một bàn tròn mà hai bạn Hải và Liên ngồi cạnh nhau.
Vậy số cách xếp chỗ ngồi sao cho Hải và Liên không ngồi cạnh nhau là: 7! – 6!.2 =6!.5.
Chọn C.

👍🏻 Cách 1.
Như trên hình là số thứ tự các ghế
❤️ Trường hợp 1
Ghế có số lẻ là ghế các bạn nữ thì
G1 có 4 lựa chọn
G3 có 3 lựa chọn
G5 có 2 lựa chọn
G1 có 1 lựa chọn
Các ghế chẵn là nam
G2 có 4 lựa chọn
G4 có 3 lựa chọn
G6 có 2 lựa chọn
G8 có 1 lựa chọn
==> Với trường hợp 1 sẽ có
(4x3x2x1)x(4x3x2x1)=576 cách xếp
❤️ Trường hợp 2
Các ghế lẻ là nam và các ghế chẵn là nữ thì tương tự ta cũng có 576 cách xếp
=> Với cách 1 ta có
2x576=1152 cách xếp
Cách 2 xếp 2 bàn ngược lại với cách 1 thì ta cũng sẽ có
1152 cách xếp
=> Với 2 cách xếp + 4 trường hợp ta có
2x1152=2304 cách xếp

Số cách xếp là:
\(\left(C^2_4\cdot C^2_4-2!\cdot2!\cdot2!\right)\cdot2=56\left(cách\right)\)

xếp ngẫu nhiên 8 bạn học sinh vào 4 bàn có 8! cách 40320 cách
=> \(n\left(\Omega\right)=40320\)
Gọi A:" có đúng 2 bàn mà trong đó mỗi bàn gồm 1 nam và 1 nữ "
=> \(n\left(A\right)=C^1_4.C^1_4..4.C^1_3.C^1_3.3.C^2_2.2.C^2_2.1=3456\) cách
=> P(A)= 3456/40320 =3/35

Số cách xếp quanh bàn tròn là \(n\left(\Omega\right)=9!\)
Kí hiệu A là biến cố : "Nam nữ ngồi xen kẽ nhau"
Ta có :
\(n\left(A\right)=4!5!\) và \(P\left(A\right)=\dfrac{4!5!}{9!}\approx0,008\)

Vì giữa 3 bạn nữ có 2 vị trí trống, để xếp thỏa yêu cầu phải có dạng A a B b C ¯ . Trong đó A, B, C là 3 bạn nữ, a, b là 2 bạn nam.
Bước 1: Chọn 2 bạn nam trong 3 bạn nam, có C 5 2 cách.
Bước 2: Gọi nhóm A a B b C ¯ là X. Xếp X và 3 bạn nam còn lại thành 1 hàng ngang có 4! cách.
Bước 2: Ứng với mỗi cách xếp ở bước 1, có 2! cách xếp các bạn nam trong X và 3! cách xếp các bạn nữ trong X.
Theo quy tắc nhân có C 4 2 . 4 ! . 3 ! . 2 ! = 2880 cách xếp thỏa yêu cầu.
Chọn C.

b. đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì Ta có một cách xếp mới . vì vậy cần chọn phương án D
Để xác định số cách xếp ta phải làm theo các công đoạn như sau.
1. Chọn 3 nam từ 6 nam. Có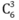 cách.
cách.
2. Chọn 2 nữ từ 5 nữ. Có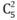 cách.
cách.
3. Xếp 5 bạn đã chọn vào bàn đầu theo những thứ tự khác nhau. có 5! Cách.
Từ đó ta có số cách xếp là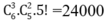
Chọn C.