Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Xảy ra hai trường hợp
TH1 : 2 câu lý thuyết, 1 câu bài tập có ![]() .
.
TH2 : 1 câu lý thuyết, 2 câu bài tập có ![]() .
.
Vậy có thể tạo 60 + 36 = 96A. 96 đề khác nhau.

Có hai phương án xây dựng đề kiểm tra như sau:
· Phương án 1: Đề gồm 1 câu hỏi dễ và 2 câu hỏi khó
Số cách chọn 1 câu hỏi dễ từ 6 câu hỏi dễ là C 6 1 , số cách chọn 2 câu hỏi khó từ 4 câu hỏi khó là C 4 2 .
Theo quy tắc nhân, số cách tạo đề kiểm tra của phương án này là C 6 1 . C 4 2 = 36
· Phương án 2: Đề gồm 2 câu hỏi dễ và 1 câu hỏi khó.
Số cách chọn 2 câu hỏi dễ từ 6 câu hỏi dễ là C 6 2 , số cách chọn 1 câu hỏi khó từ 4 câu hỏi khó là C 4 1 .
Theo quy tắc nhân, số cách tạo đề kiểm tra của phương án này là C 6 2 . C 4 1 = 60
Vậy theo quy tắc cộng thì số đề kiểm tra có thể lập được là : 36 + 60 = 96.
Chọn D.

http://www.toanhocnhatrang.com/2015/05/bai-toan-so-298.html
Gọi A là tập hợp cách chọn đề có 3 câu dễ, 1 câu khó, 1 câu trung bình.
B là tập hợp cách chọn đề có 2 câu dễ, 2 câu khó, 1 câu trung bình
C là tập hợp cách chọn đề có 2 câu dễ, 1 câu khó, 2 câu trung bình
D là tập hợp cách chọn đề thỏa mãn yêu cầu đề ra. Ta có:
D = A \(\cup\) B \(\cup\) C
ngoài ra A,B,C đôi một không giao nhau. Theo quy tắc cộng ta có
\(\left|D\right|\) = \(\left|A\right|\) + \(\left|B\right|\) + \(\left|C\right|\) (1)
Theo quy tắc nhân ta có
\(\left|A\right|\) = \(C_{15}^3\).\(C_5^1\).\(C_{10}^1\) = 22750
\(\left|B\right|\) = \(C_{15}^2\).\(C_5^2\).\(C_{10}^1\) = 10500
\(\left|C\right|\) = \(C_{15}^2\).\(C_5^1\).\(C_{10}^2\) = 23625
Thay vào (1) ta có \(\left|D\right|\) = 56875
Vậy có 56875 cách chọn đề kiểm tra.

TH1: chọn \(1\)câu khó từ \(5\)câu: \(C^1_5\).
Chọn \(9\)câu trong đó có cả câu trung bình và câu dễ.
Ta sử dụng phần bù. Số cách là: \(C^9_{45}-C^9_{20}-C^9_{25}\).
TH cách số câu khó từ \(2\)đến \(5\)ta làm tương tự.
Khi đó có tổng số cách chọn \(10\)câu sao cho đủ 3 loại câu hỏi là:
\(C^1_5\left(C^9_{45}-C^9_{20}-C^9_{25}\right)+C^2_5\left(C^8_{45}-C^8_{20}-C^8_{25}\right)+C^3_5\left(C^7_{45}-C^7_{20}-C^7_{25}\right)\)
\(+C^4_5\left(C^6_{45}-C^6_{20}-C^6_{25}\right)+C^5_5\left(C^5_{45}-C^5_{20}-C^5_{25}\right)=7052230625\)

Đáp án A
Số cách sắp xếp 50 câu cho một đề thi là 50!
Số cách chọn 20 câu nhận biết để xếp chúng vào đầu tiên là: 20!
Số cách chọn 10 câu thông hiểu để xếp chúng vào vị trí thứ hai là 10!
Số cách chọn 15 câu vận dụng để xếp chúng vào vị trí thứ ba là 15!
Số cách chọn 5 câu vận dụng cao xếp chúng vào vị trí cuối cùng là 5!
=> Xác suất cần tìm được tính bằng: P = 20 ! . 10 ! . 15 ! . 5 ! 50 ! = 4,56.10-26
=> Chọn phương án A.

Đáp án A
Ta xét 2 trường hợp
TH1:
Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được
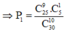
TH2:
Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được
![]()
Vậy xác suất cần tính là
![]()

