Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


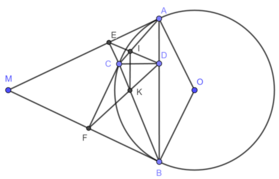

( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)


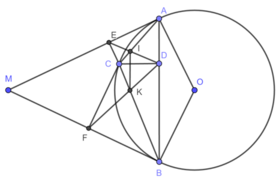

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)


1) Hình vẽ câu 1) đúng
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B
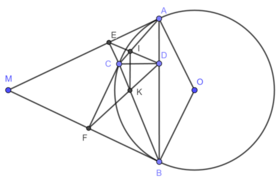

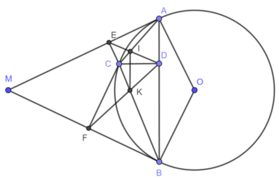

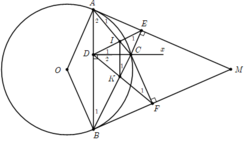
Vì \(\left\{{}\begin{matrix}CD\perp AB\\CE\perp MA\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{ADC}=90^o\\\widehat{AEC}=90^o\end{matrix}\right.\) \(\Rightarrow\widehat{ADC}+\widehat{AEC}=180^o\)
Xét tứ giác AECD có: \(\widehat{ADC}+\widehat{AEC}=180^o\left(cmt\right)\)
\(\Rightarrow\) Tứ giác AECD nội tiếp
\(\Rightarrow\widehat{EAC}=\widehat{EDC}\) ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét (O) có:
\(\widehat{EAC}\) là góc tạo bởi tia tiếp tuyến và dây cung và \(\widehat{ABC}\) là góc nội tiếp cùng chắn cung AC
\(\Rightarrow\widehat{EAC}=\widehat{ABC}\) ( Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{EDC}\)