Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

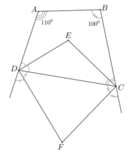
Trong tứ giác ABCD, ta có: ∠ A + ∠ B + ∠ C + ∠ D = 360 °
⇒ ∠ C + ∠ D = 360 ° - ( ∠ A + ∠ B) = 360 ° – ( 110 ° + 100 ° ) = 150 °
Do DE và CE lần lượt là tia phân giác của góc 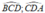
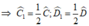
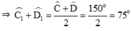
Trong ΔCED ta có:
∠ CED = 180o – ∠ C 1 + ∠ D 1 = 180 ° - 75 ° = 105 °
DE ⊥ DF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ EDF = 90 °
CE ⊥ CF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ ECF = 90 °
Trong tứ giác CEDF, ta có: ∠ DEC + ∠ EDF + ∠ DFC + ∠ ECF = 360 °
⇒ ∠ DFC = 360 ° - ( ∠ DEC + ∠ EDF + ∠ ECF) = 360 ° - 105 ° - 90 ° - 90 ° = 75 °

Ta có: góc A+B+C+D=360 =>C+D=150 độ
Tính góc CED + EDC=1/2C+1/2D=1/2(C+D)=75(do phân giác)
=>E=180-75=105
ta có góc tạo bởi 2 tia phân giác của 2 góc kề có tổng là 90 độ (có cm trong sgk)
nên ECF+EDF=90+80=180 độ
=>CFD= 360-180-105=75
Xong rồi, nhưng bạn lập luận chặt chẽ hơn nhé

Tứ giác ABCD có A^+B^+C^+D^=360độ
D^+C^=150độ
\(\frac{1}{2}\)D^+\(\frac{1}{2}\)C^=\(\frac{150}{2}\)độ
\(\Rightarrow\)D2^+C2^=\(\frac{150}{2}\)=75độ
Tam giác DEC có D2^+C2^+CED^=180độ
CED^=105độ

Ta có: góc A+B+C+D=360
\(\Rightarrow\)C+D=150 độ
Tính góc CED + EDC=1/2C+1/2D=1/2(C+D)=75(do phân giác)
\(\Rightarrow\)E=180-75=105
Ta có góc tạo bởi 2 tia phân giác của 2 góc kề có tổng là 90 độ (có cm trong sgk)
Nên ECF+EDF=90+80=180 độ
\(\Rightarrow\)CFD= 360-180-105=75
giải hộ bài này với
ai piet giai ho gium mink ik ma!!!