Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Tam giác ABC có MN // BC \(\left(M\in AB;N\in AC\right)\)=> Tam giác AMN 
tam giác ABC
Tam giác ABC có ML // AC \(\left(M\in AB;L\in BC\right)\)=> Tam giác MBL tam giác ABC
Tam giác AMN tam giác ABC ; tam giác MBL tam giác ABC = >Tam giác AMN MBL
b, Tam giác AMN tam giác ABC , ta có :
\(\widehat{A} chung ,\widehat{AMN}=\widehat{B} ; \widehat{ANC}=\widehat{C}\)
\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)
Tỉ số đồng dạng \(k=\frac{AM}{AB}=\frac{1}{3}\)( Vì AM = \(\frac{1}{2}\)MB )
Tam giác AMNtam giác ABC có :
\(\widehat{B}\)chung ; \(\widehat{BML}=\widehat{A}\); \(\widehat{MLB}=\widehat{C}\)
\(\frac{BM}{BA}=\frac{BL}{BC}=\frac{ML}{AC}\)
Tỉ số đồng dạng \(k'=\frac{BM}{BA}=\frac{2}{3}\)
Tam giác AMN tam giác MBL , ta có :
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{BLM};\widehat{A}=\widehat{BLM}\)
\(\frac{AM}{MB}=\frac{AN}{ML}=\frac{MN}{BL}\)
=> Tiwr số đồng dạng \(k''=\frac{AM}{MB}=\frac{1}{2}\)
a) MN // BC => ∆AMN ∽ ∆ABC
ML // AC => ∆MBL ∽ ∆ABC
và ∆AMN ∽ ∆MLB
b)
∆AMN ∽ ∆ABC có:
= ; =
=
∆MBL ∽ ∆ABC có:
= , chung, =
=
∆AMN ∽ ∆MLB có:
= , = , =
a, Tam giác AMN ~ Tam giác ABC
Tam giác MBL ~ tam giác ABC
Tam giác AMN ~ tam giác MBL
Kiếm trên mạng ấy, nhiều lắm đó bạn.
https://www.google.com/search?q=T%E1%BB%AB+%C4%91i%E1%BB%83m+M+thu%E1%BB%99c+c%E1%BA%A1nh+AB+c%E1%BB%A7a+tam+gi%C3%A1c+ABC+v%E1%BB%9Bi+AM+%3D+1+2+12+MB%2C+k%E1%BA%BB+c%C3%A1c+tia+song+song+v%E1%BB%9Bi+AC+v%C3%A0+BC%2C+ch%C3%BAng+c%E1%BA%AFt+BC+v%C3%A0+AC+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+t%E1%BA%A1i+L+v%C3%A0+N+a%2C+N%C3%AAu+t%E1%BA%A5t+c%E1%BA%A3+c%C3%A1c+c%E1%BA%B7p+tam+gi%C3%A1c+%C4%91%E1%BB%93ng+d%E1%BA%A1ng+b%2C+%C4%91%E1%BB%91i+v%E1%BB%9Bi+m%E1%BB%97i+c%E1%BA%B7p+tam+gi%C3%A1c+%C4%91%E1%BB%93ng+d%E1%BA%A1ng%2C+h%C3%A3y+vi%E1%BA%BFt+c%C3%A1c+c%E1%BA%B7p+g%C3%B3c+b%E1%BA%B1ng+nhau+v%C3%A0+t%E1%BB%89+s%E1%BB%91+%C4%91%E1%BB%93ng+d%E1%BA%A1ng+t%C6%B0%C6%A1ng+%E1%BB%A9ng&oq=T%E1%BB%AB+%C4%91i%E1%BB%83m+M+thu%E1%BB%99c+c%E1%BA%A1nh+AB+c%E1%BB%A7a+tam+gi%C3%A1c+ABC+v%E1%BB%9Bi+AM+%3D%C2%A0++1+2+12+MB%2C+k%E1%BA%BB+c%C3%A1c+tia+song+song+v%E1%BB%9Bi+AC+v%C3%A0+BC%2C+ch%C3%BAng+c%E1%BA%AFt+BC+v%C3%A0+AC%C2%A0l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+t%E1%BA%A1i+L+v%C3%A0+N++a%2C+N%C3%AAu+t%E1%BA%A5t+c%E1%BA%A3+c%C3%A1c+c%E1%BA%B7p+tam+gi%C3%A1c+%C4%91%E1%BB%93ng+d%E1%BA%A1ng%C2%A0++b%2C+%C4%91%E1%BB%91i+v%E1%BB%9Bi+m%E1%BB%97i%C2%A0c%E1%BA%B7p+tam+gi%C3%A1c+%C4%91%E1%BB%93ng+d%E1%BA%A1ng%2C+h%C3%A3y+vi%E1%BA%BFt+c%C3%A1c+c%E1%BA%B7p+g%C3%B3c+b%E1%BA%B1ng+nhau+v%C3%A0+t%E1%BB%89+s%E1%BB%91+%C4%91%E1%BB%93ng+d%E1%BA%A1ng+t%C6%B0%C6%A1ng+%E1%BB%A9ng&aqs=chrome..69i57&sourceid=chrome&ie=UTF-8
`a,` Các cặp tam giác đồng dạng là :
\(\Delta AMN\sim\Delta ABC\) `(` vì \(MN\text{/}\text{/}BC\) `)`
\(\Delta ABC\sim\Delta MBL\) `(` vì \(ML\text{/}\text{/}AC\) `)`
\(\Delta AMN\sim\Delta MBL\)
`b,` * \(\Delta AMN\sim\Delta ABC\) thì
\(\left\{{}\begin{matrix}\widehat{MAN}=\widehat{BAC}\\\widehat{AMN}=\widehat{ABC}\\\widehat{ANM}=\widehat{ACB}\end{matrix}\right.\)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
* \(\Delta ABC\sim\Delta MBL\) thì
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{BML}\\\widehat{ABC}=\widehat{MBL}\\\widehat{ACB}=\widehat{MLB}\end{matrix}\right.\)
\(\dfrac{AB}{MB}=\dfrac{BC}{BL}=\dfrac{AC}{ML}\)
* \(\Delta AMN\sim\Delta MBL\) thì
\(\left\{{}\begin{matrix}\widehat{MAN}=\widehat{BML}\\\widehat{AMN}=\widehat{MBL}\\\widehat{ANM}=\widehat{MLB}\end{matrix}\right.\)
\(\dfrac{AM}{MB}=\dfrac{AN}{ML}=\dfrac{MN}{BL}\)
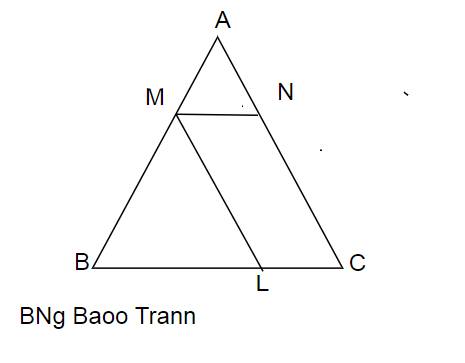
a) MN // BC => ∆AMN ∽ ∆ABC
ML // AC => ∆MBL ∽ ∆ABC và ∆AMN ∽ ∆MLB
b) ∆AMN ∽ ∆ABC có:
= ; =
=
∆MBL ∽ ∆ABC có:
= , chung, =
=
∆AMN ∽ ∆MLB có:
= ,
a) ΔAMN∼ΔABC
ΔBML∼ΔBAC
b) Ta có: ΔAMN∼ΔABC(cmt)
nên \(\widehat{AMN}=\widehat{ABC}\); \(\widehat{ANM}=\widehat{ACB}\); \(\widehat{A}\) chung và \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
Ta có: ΔBML∼ΔBAC(cmt)
nên \(\widehat{BML}=\widehat{BAC}\); \(\widehat{BLM}=\widehat{BCA}\); \(\widehat{B}\) chung và \(\dfrac{BM}{BA}=\dfrac{ML}{AC}=\dfrac{BL}{BC}\)
a) ΔABC có MN // BC (M ∈ AB; N ∈ AC) ⇒ ΔAMN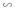
ΔABC.
ΔABC có ML // AC (M ∈ AB; L ∈ BC) ⇒ ΔMBL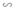
ΔABC
ΔAMN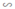
ΔABC; ΔMBL 
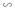ΔABC ⇒ ΔAMN 
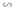ΔMBL.
b) ΔAMN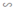
ΔABC có:
ΔMBL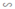
ΔABC có:
ΔAMN
ΔMBL có: