Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số có 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 luôn đứng cạnh nhau.
Đặt y=12 khi đó x có dạng ![]() với a;b;c;d;e đôi một khác nhau và thuộc tập {y;3;4;5;6} nên có
với a;b;c;d;e đôi một khác nhau và thuộc tập {y;3;4;5;6} nên có
Khi hoán vị hai số1;2 ta được một số khác nên có 120.2=240 số x.
Vậy số thỏa yêu cầu bài toán là: P6 - 240 =480số.
Chọn B.

Đáp án A
Xếp một hàng thành 6 ô đánh số từ 1 đển 6 như hình bên:
Số các chữ số gồm 6 chữ số khác nhau được lập từ 6 chữ số đã cho là 5.5! = 600 số.
Ta tìm số các số mà hai chữ số 0 và 5 đứng cạnh nhau:
• Chữ số 0 và 5 cạnh nhau tại ô số 1 và 2 có 1.4! = 24 số.
• Chữ số 0 và 5 đứng cạnh nhau tại các ô (2;3), (3;4), (4;5), (5;6) có 4.2!.4! = 192 số.
Vậy có tất cả 24 + 192 = 216 số mà chữ số 0 và 5 đứng cạnh nhau.
Do đó, số các số thỏa mãn yêu cầu bài toán là 600 – 216 = 384 số.

Chọn C
Số cách chọn 3 số bất kì từ tập {4;5;6;7} là C 3 4
Do 1, 2, 3 luôn đứng cạnh nhau nên ta xem chúng như một phần tử.
Số các số tự nhiên có sáu chữ số đôi một khác nhau trong đó 1, 2, 3 luôn đứng cạnh nhau là 4!. C 3 4 .3! = 576 số.

Vì có 3 số lẻ là 1,3,5, nên ta tạo được 6 cặp số kép: 13;31;15;51;35;53
Gọi A là tập các số gồm 4 chữ số được lập từ X={0;13;2;4;6}.
Gọi A1,A2,A3 tương ứng là số các số tự nhiên lẻ gồm 4 chữ số khác nhau được lập từ các chữ số của tập X và 13 đứng ở vị trí thứ nhất, thứ hai và thứ ba.
Ta có: ![]()
Nên ![]()
Vậy số các số cần lập là: 6.60=360 số.
Chọn A.

Gọi số cần lập là ![]()
Vì a khác 1 nên a có 5 cách chọn. Ứng với mỗi cách chọn a ta có: ![]() cách chọn b;c;d.
cách chọn b;c;d.
Vậy có ![]() số .
số .
chọn A.

Gọi x là số có 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 luôn đứng cạnh nhau.
Đặt y=12 khi đó x có dạng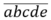 với a;b;c;d;e đôi một khác nhau và thuộc tập {y;;3;4;5;6} nên có 5!=120 số.
với a;b;c;d;e đôi một khác nhau và thuộc tập {y;;3;4;5;6} nên có 5!=120 số.
Khi hoán vị hai số 1;2 ta được một số khác nên có 120.2=240 số
Vậy số thỏa yêu cầu bài toán là: 6!-240=480 số.
Chọn B.