Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Từ bảng kết luận của bài trước hãy dùng các đẳng thức b = 2b’, Δ = 4Δ’ để suy ra những kết luận sau:

Với b = 2b’, Δ = 4Δ’ ta có:
a) Nếu Δ' > 0 thì Δ > 0 phương trình có hai nghiệm
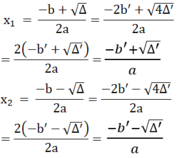
b) Nếu Δ' = 0 thì Δ = 0 phương trình có nghiệm kép
x = (-b)/2a = (-2b')/2a = (-b')/a
c) Nếu Δ' < 0 thì Δ < 0 do đó phương trình vô nghiệm.

a) Nếu Δ > 0 thì từ phương trình (2) suy ra x + b/2a = ± √Δ/2a
Do đó,phương trình (1) có hai nghiệm x 1 = ( - b + √ Δ ) / 2 a ; x 2 = ( - b - √ Δ ) / 2 a
b) Nếu Δ = 0 thì từ phương trình (2) suy ra ( x + b / 2 a ) 2 = 0
Do đó,phương trình (1) có nghiệm kép x = (-b)/2a

Nếu Δ = 0 thì từ phương trình (2) suy ra (x + b/2a)2 =0
Do đó,phương trình (1) có nghiệm kép x = (-b)/2a

Nếu Δ > 0 thì từ phương trình (2) suy ra x + b/2a = ± √Δ/2a
Do đó,phương trình (1) có hai nghiệm x1 = (-b + √Δ)/2a; x2 = (-b-√Δ)/2a

- Đồ thị nằm ở phía dưới trục hoành
- Các cặp điểm M và M’; N và N’; P và P’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm cao nhất của đồ thị.

- Đồ thị nằm ở phía dưới trục hoành
- Các cặp điểm M và M’; N và N’; P và P’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm cao nhất của đồ thị.

Đường tròn bán kính R (ứng với cung 360 ° ) có độ dài là 2πR
Vậy cung
1
đ
ộ
, bán kính R có độ dài là 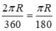
Suy ra cung
n
°
, bán kính R có độ dài là 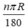
Với b = 2b’, Δ = 4Δ’ ta có:
Nếu Δ' > 0 thì Δ > 0 phương trình có hai nghiệm