Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒vân trung tâm O là một vân trùng. Tại điểm M ≠O trên màn vân sáng của hai bức xạ trùng nhau thì ta có OM = k 1 i 1 = k 2 i 2 ( k 1 , k 2 nguyên dương)
⇒ k 1 λ 1 = k 2 λ 2 ⇒ k 1 k 2 = λ 2 λ 1 = 5 6 ⇒ k 1 chia hết cho 5, k 2 chia hết cho 6.
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
i’ = k 1 min . i 1 = 5. λ 1 D a = 6 m m , các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm.
Ta có L 2. i ' = 2 , 33
→ số vân trùng của hai bức xạ trên màn bằng n = 2 L 2 i ' + 1 = 2.2 + 1 = 5 vân.

Đáp án D
+ Khi hai bức xạ trùng nhau thì:
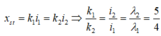
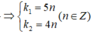
+ Vị trí vân sáng trùng được xác định bởi:
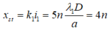
+ Màn có bề rộng L = 9 mm nên:
![]()
![]()
n= -1; 0;1

Đáp án A
Tổng số vân sáng mà hai hệ vân cho được là 33 + 5 = 38
+ Số vân sáng của bức xạ λ 1 cho trên màn
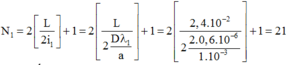
Vậy số vân sáng của bức xạ λ 2 trên màn sẽ là 38 – 21 = 17
→ Tại vị trí biên vân sáng bậc 10 của bức xạ λ 1 trùng với vân sáng bậc 8 của bức xạ λ 2
![]()

Đáp án B
*Xét tỉ số:  => Vân sáng bậc 5 của bức xạ 1 trùng với vân sáng bậc 6 của bức xạ 2.
=> Vân sáng bậc 5 của bức xạ 1 trùng với vân sáng bậc 6 của bức xạ 2.
*Khoảng cách nhỏ nhất giữa hai vân sáng quan sát được trên màn được tính bởi
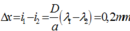
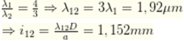



Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒ vân trung tâm O là một vân trùng. Tại điểm M ≠ O trên màn vân sáng của hai bức xạ trùng nhau thì ta có
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm
→ số vân trùng của hai bức xạ trên màn bằng
Đáp án A