Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Xét tỉ số:
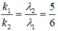
Vân sáng bậc 5 của bức xạ 1 trùng với vân sáng bậc 6 của bức xạ 2.
Khoảng cách nhỏ nhất giữa hai vân sáng quan sát được trên màn được tính bởi
![]()
![]()

Đáp án D
Phương pháp: Công thức xác định vị trí vân tối x t = k + 1 2 λ D a
Cách giải: Ta có:
 Mà
Mà 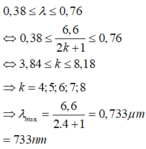

Đáp án C
+ Khoảng vân giao thoa của hai bức xạ i 1 = D λ 1 a = 2 . 450 . 10 - 9 0 , 5 . 10 - 3 = 1 , 8 m m
i 2 = D λ 2 a = 2 . 600 . 10 - 9 0 , 5 . 10 - 3 = 2 , 4 m m
+ Các vị trí hệ hai vân sangs trùng nhau x 1 = x 2 ⇒ k 1 k 2 = i 1 i 2 = 2 , 4 1 , 8 = 4 3
cứ sau mỗi khoảng i 12 = 4 i 1 = 7 , 2 m m lại có một vị trí trùng nhau của hệ hai vân sang.
Xét tỉ số M N i = 22 - 5 , 5 7 , 2 = 2 , 3 ->có hai vân sáng trùng nhau

Đáp án C
+ Điều kiện trùng nhau của hai bức xạ: 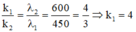
+ Khoảng cách từ vân chính giữa đến vân gần nhất cùng màu với vân chính giữa là
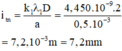
+ Trên đoạn MN, số vị trí vân sáng trùng nhau của hai bức xạ thỏa mãn:
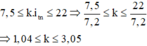
Có 2 giá trị k thỏa mãn => Có 2 vân trùng nhau trên đoạn MN

Chọn đáp án B
Xét tỉ số: k 1 k 2 = λ 1 λ 2 = 5 6 . Vân sáng bậc 5 của bức xạ 1 trùng với vân sáng bậc 6 của bức xạ 2.
Khoảng cách nhỏ nhất giữa hai vân sáng quan sát được trên màn được tính bởi Δ x = i 1 − i 2 = D a λ 1 − λ 2 = 0 , 2 m m

Đáp án C
+ Điều kiện để có sự trùng nhau của hai hệ vân sáng k 1 k 2 = λ 2 λ 1 = 600 450 = 4 3
→ i 12 = 4 i 1 = 7 , 2 m m
Xét tỉ số O M i 12 = 5 , 5 7 , 2 = 0 , 76 O N i 12 = 22 7 , 2 = 3 , 05 → có 3 vân trùng
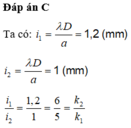



Đáp án D