Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

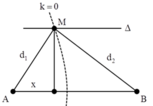
+ Để M là cực tiểu và gần trung trực của của AB nhất thì M phải nằm trên cực tiểu ứng với k = 0.
→ d2 – d1 = (0 + 0,5)λ = 1 cm.
Từ hình vẽ, ta có:
d 1 2 = 2 2 + x 2 d 2 2 = 2 2 + 8 − x 2 → 2 2 + 8 − x 2 − 2 2 + x 2 = 1
→ Giải phương trình trên ta thu được x = 3,44 cm.
Vậy khoảng cách ngắn nhất giữa M và trung trực AB là 4 – 3,44 = 0,56 cm.
Đáp án A

Chọn đáp án A
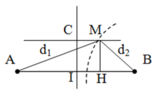
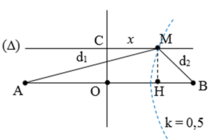
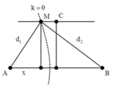
Gọi C M = I H = x
Trên hình ta có
d 1 = A H 2 + M H 2 = 4 + x 2 + 2 2 (1)
d 2 = B H 2 + M H 2 = 4 − x 2 + 2 2 (2)
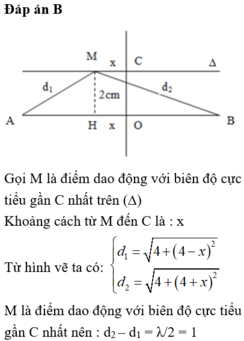
Vì M cực tiểu nên có. d 1 − d 2 = k + 1 2 λ . Vì cực tiểu gần C nhất nên là cực tiểu thứ nhất, nhận k=0
Vậy có. d 1 − d 2 = 1 c m (3).
Thay (1), (2) vào (3) → 4 + x 2 + 2 2 − 4 − x 2 + 2 2 = 1
Giải phương trình ta được CM = x = 0,56cm.

Đáp án B
Gọi CM = IH = x
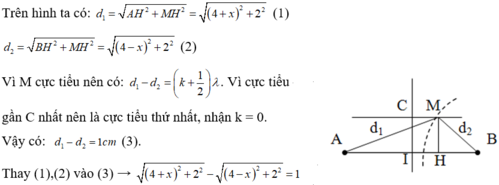
Giải phương trình ta được CM = x = 0,56cm.

Đáp án D
+ Số dãy cực đại trên đoạn
![]()
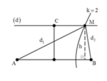
+ Để CM là lớn nhất thì M thuộc hypebol ứng với k=2
Ta có d 1 - d 2 = 8 cm
+ Với:
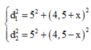
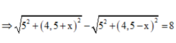
![]()


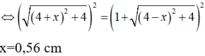

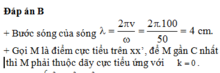
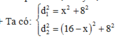
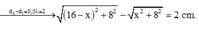
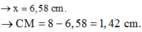
Đáp án A
+ Tần số góc của khung dây ω = 2 πn = 2 π . 50 = 100 π rad / s rad/s
→ Suất điện động cảm ứng cực đại
E 0 = ωNBS = 100 π . 500 . 2 5 π . 220 . 10 - 4 = 220 2 V .