Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

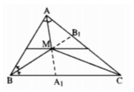
Ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc trong một tam giác).
Suy ra: ∠C = 180º – (∠A + ∠B)
Do ba đường phân giác của một tam giác đồng quy tại một điểm nên CM là tia phân giác của góc C.
Ta có ½. (∠A + ∠B ) = ∠(MAB) + ∠(MBA) = 180 − ∠(AMB) = 180o − 111o = 69o.
Suy ra ∠A + ∠B = 138o
Suy ra ∠C = 180o – (∠A + ∠B) = 180o − 138o = 42o.
Vì CM là tia phân giác của góc ACB nên: ∠(ACM) = ∠(BCM) = 420 : 2 = 21o.

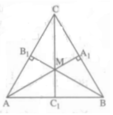
Ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc trong một tam giác).
Suy ra: ∠C = 180º – (∠A + ∠B)
Do ba đường phân giác của một tam giác đồng quy tại một điểm nên CM là tia phân giác của góc C.
1/2(∠A + ∠B ) = ∠(MAB) + ∠(MBA) = 180 − ∠(AMB) = 180o − 136o = 44o
Suy ra ∠A + ∠B = 2.44o = 88o
∠C = 180o − 88o = 92o
Vậy ∠(ACM) = ∠(BCM) = 92o : 2o = 46o

Gọi giao điểm của CM và AB là C1. Ta cần chứng minh CC1 ⊥ AB và C1 là trung điểm của đoạn thẳng AB. Vì trong một tam giác ba đường cao đồng quy nên CM hay CC1 vuông góc với AB.
+) Do tam giác ABC cân tại C có CM là đường cao nên CM đồng thời là đường trung trực của đoạn thẳng AB ( tính chất tam giác cân).

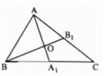
+) Vì tam giác ABC có hai đường trung tuyến AA1 và BB1 cắt nhau tại O nên O là trọng tâm tam giác ABC.
Theo tính chất trọng tâm tam giác ta có: 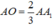
+) Ta có: 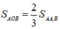
( vì có cùng chiều cao hạ từ B và 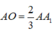 )
)
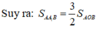
Và 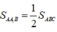 ( vì có cùng chiều cao hạ từ A và
( vì có cùng chiều cao hạ từ A và 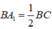 ).
).
+) Từ đó suy ra:
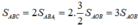
Nếu SAOB = 5cm2 thì SABC = 3.5 = 15(cm2)

Xét ΔABC có các đường trung tuyến \(AA_1;BB_1\) cắt nhau tại O
nên O là trọng tâm
=>AO=2/3AA1
\(\Leftrightarrow S_{AA_1B}=\dfrac{2}{3}S_{AOB}\)
\(\Leftrightarrow S_{ABC}=3\cdot S_{AOB}=15\left(cm^2\right)\)

Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
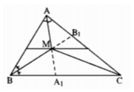
làm khác cách trong vở bài tập nha!