
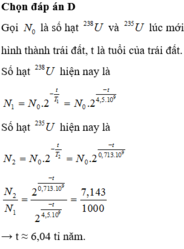
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

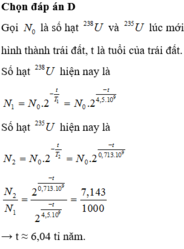

Khối lượng còn lại của hai đồng vị sau thời gian t là
\(m(238) = m_{0238}.2^{-t/T_1}.\\ m(235) = m_{0235}.2^{-t/T_2}.\)
Chi hai phương trình ta thu được
\(\frac{m(238)}{m(235)} = 2^{t(\frac{1}{T_2}-\frac{1}{T_1})}.(2)\)
mà hiện tại tỉ số khối lượng của chúng là \(\frac{92,848}{7,142} = 13.\)
Thay vào phương trình (2) ta được \(2^{t(1/T_2-1/T_1)} = 13 => t (1/T_2-1/T_1) = \ln_2{13} => t \approx 3,1.10^9\) năm.
Vậy tuổi Trái Đất cỡ 3,1 tỷ năm.

Kí hiệu \(N_{01}\), \(N_{02}\) là số hạt ban đầu lần lượt của \(^{235}U\) và \(^{238}U\).
Hiện nay \(t_2\): \(\frac{N_{1}}{N_{2}}=\frac{N_{01}2^{-\frac{t_2}{T_1}}}{N_{02}2^{-\frac{t_2}{T_2}}} =\frac{7}{1000}.(1)\)
Thời điểm \(t_1\):
\(\frac{N_1}{N_2}= \frac{N_{01}2^{-\frac{t_1}{T_1}}}{N_{02}2^{-\frac{t_1}{T_2}}} = \frac{3}{100}.(2)\)
Chia (1) cho (2) => \(\frac{2^{-\frac{t_2}{T_1}}.2^{-\frac{t_1}{T_2}}}{2^{-\frac{t_1}{T_1}}.2^{-\frac{t_2}{T_2}}}= \frac{7.100}{3.1000}= \frac{7}{30}.\)
Áp dụng \(\frac{1}{2^{-x}} =2^x. \)
=> \(2^{(t_2-t_1)(\frac{1}{T_2}-\frac{1}{T_1})} = \frac{7}{30}.\)
=> \(t_2-t_1 = \frac{T_1T_2}{T_1-T_2}\ln_2 (7/30)=1,74.10^{9}\).(năm) \(= 1,74 \)(tỉ năm).
Như vậy cách hiện nay 1,74 tỉ năm thì trong urani tự nhiên có tỉ lệ số hạt thỏa mãn như bài cho.