Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu này đáp án là đenta phi= (2n+1)lamđa/2 chắc chắn không đúng vì vế trái là đơn vị góc còn vế phải lại là độ dài.
Bạn xem lại câu hỏi xem có thiếu sót gì không nhé.
Gọi \(\Delta\varphi\) là độ lệch pha dao động của 2 sóng truyền tới M.
Vì dao động tại M là tổng hợp của dao động do 2 sóng truyền đến nên M dao động cực đại khi độ lệch pha 2 sóng này là nguyên lần \(2\pi\) (tương đương như 2 dao động cùng pha).
\(\Rightarrow\Delta\varphi=n.2\pi\) (n nguyên).

Đáp án B
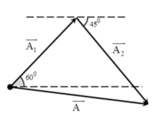
Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Cách giải:
- Phương trình dao động của x; x1; x2: 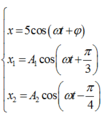
Suy ra :
+ Độ lệch pha giữa x và x1 là :![]()
+ Độ lệch pha giữa x và x2 là : 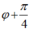
+ Độ lệch pha giữa x1 và x2 là : 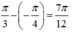
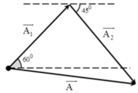
=> Ta có giản đồ vecto :
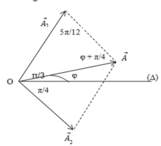
- Áp dụng định lí hàm số sin trong tam giác ta có:
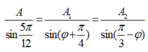
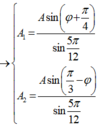
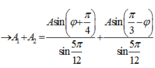
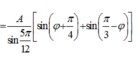
có: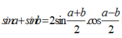
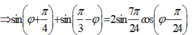
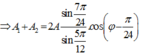
Để [A1 + A2] đạt cực đại thì 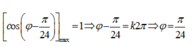

Đáp án C
Với hai nguồn cùng pha, phần tử tại M dao động với biên độ cực đại khi hiệu đường đi của hai sóng từ hai nguồn truyền tới M bằng một số nguyên lần bước sóng

Chọn đáp án C
+ Với hai nguồn cùng pha, phần tử tại M dao động với biên độ cực đại khi hiệu đường đi của hai sóng từ hai nguồn truyền tới M bằng một số nguyên lần bước sóng.

Đáp án C
Với hai nguồn cùng pha, phần tử tại M dao động với biên độ cực đại khi hiệu đường đi của hai sóng từ hai nguồn truyền tới M bằng một số nguyên lần bước sóng

Đáp án B
![]()
![]()
![]()
→ Ta luôn có
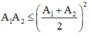
→ Tích A1 A2 nhỏ nhất khi (A1 = A2) khi đó tổng (A1 + A2) là lớn nhất
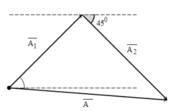
→ Các vectơ hợp thành tam giác cân.
+ Từ hình vẽ ta có:
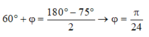

- Với x = x1 + x2:
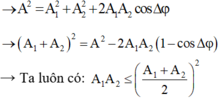
⇒ Tích A1A2 nhỏ nhất khi A1 = A2 khi đó tổng A1 + A2 là lớn nhất → Các vectơ hợp thành tam giác cân:
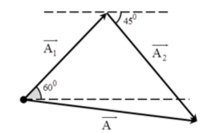
- Từ hình vẽ ta có:
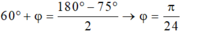
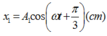

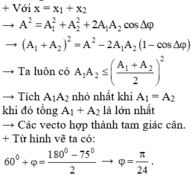
Biên độ giao động cực đại:
▲φ =2n\(\pi\) n nguyên => chọn A