Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì $G$ là trọng tâm $ABC$ nên:
$x_G=\frac{x_A+x_B+x_C}{3}=0$
$y_G=\frac{y_A+y_B+y_C}{3}=\frac{2}{3}$
ĐT cần tìm song song với trục tung nên nhận vecto pháp tuyến $(1,0)$
Do đó PTĐT cần tìm có dạng $1(x-0)+0(y-\frac{2}{3})=0$ hay $x=0$ hay chính là trục tung (??)

Gọi G là trọng tâm tam giác \(\Rightarrow G\left(\dfrac{10}{3};\dfrac{1}{3}\right)\)
Đường thẳng song song trục hoành nên nhận \(\left(0;1\right)\) là 1 vecto pháp tuyến
Phương trình:
\(0\left(x-\dfrac{10}{3}\right)+1\left(y-\dfrac{1}{3}\right)=0\Leftrightarrow y-\dfrac{1}{3}=0\)

a)
– Tọa độ trọng tâm G của tam giác ABC là:
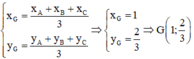
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 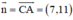 là một vtpt
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 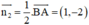 là một vtpt
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
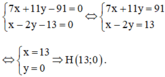
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
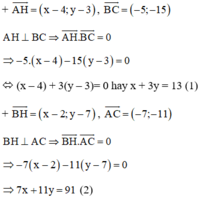
Từ (1) và (2) ta có hệ phương trình
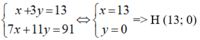
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
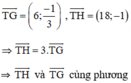
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
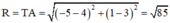
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85

Đáp án C
Gọi (d) là đường thẳng cần tìm. Do d song song với AC nên d nhận A C → ( 2 ; - 3 ) làm VTCP.
Suy ra n → ( 3 ; 2 ) là VTPT của (d) .
Do đó; đường thẳng ( d) có phương trình:
3( x- 0) +2( y-4) = 0 hay 3x+ 2y- 8=0

Do G là trọng tâm tam giác nên tọa độ G là: \(\left\{{}\begin{matrix}x_G=\frac{x_A+x_B+x_C}{3}=0\\y_G=\frac{y_A+y_B+y_C}{3}=\frac{2}{3}\end{matrix}\right.\)
\(\Rightarrow G\left(0;\frac{2}{3}\right)\)
\(\Rightarrow G\) nằm trên trục tung
\(\Rightarrow\) Không tồn tại được thẳng đi qua G và song song trục tung