Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(C): (x-1)^2+(y+2)^2=4
=>R=2; I(1;-2)
Vì (d)//Δ nên (d): 4x-3y+c=0
\(d\left(I;\left(d\right)\right)=2\)
=>\(\dfrac{\left|1\cdot4+\left(-2\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=2\)
=>|c+4+6|=10
=>|c+10|=10
=>c=0 hoặc c=-20
=>4x-3y=0 hoặc 4x-3y-20=0

(d')//(d)
=>(d'): 4x-3y+c=0
(C): x^2-4x+4+y^2+6y+9-16=0
=>(x-2)^2+(y+3)^2=16
=>R=4; I(2;-3)
Theo đề, ta có: d(I;(d'))=4
=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
=>|c+17|=4*5=20
=>c=3 hoặc c=-37

(x-1)^2+(y+2)^2=10
=>R=căn 10; I(1;-2)
Vì (d)//x+3y-5=0
nên (d): x+3y+c=0
Theo đề, ta có: d(I;(d))=can 10
=>\(\dfrac{\left|1\cdot1+3\cdot\left(-2\right)+c\right|}{\sqrt{1^2+3^2}}=\sqrt{10}\)
=>|c-5|=10
=>c=15 hoặc c=-5

1: Gọi I(0,y) là tâm cần tìm
Theo đề, ta có: IA=IB
=>\(\left(0-3\right)^2+\left(5-y\right)^2=\left(1-0\right)^2+\left(-7-y\right)^2\)
=>y^2-10y+25+9=y^2+14y+49+1
=>-10y+34=14y+50
=>-4y=16
=>y=-4
=>I(0;-4)
=>(x-0)^2+(y+4)^2=IA^2=90
2: Gọi (d1) là đường thẳng cần tìm
Vì (d1)//(d) nên (d1): 4x+3y+c=0
Theo đề, ta có: d(I;(d1))=3 căn 10
=>\(\dfrac{\left|0\cdot4+\left(-4\right)\cdot3+c\right|}{5}=3\sqrt{10}\)
=>|c-12|=15căn 10
=>\(\left[{}\begin{matrix}c=15\sqrt{10}+12\\c=-15\sqrt{10}+12\end{matrix}\right.\)

a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:
$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$
Với I là tâm đường tròn, A là điểm trên đường tròn.
Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$
Thay vào công thức ta được:
$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$
Vậy bán kính của đường tròn là $\sqrt{34}$.
Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:
$(x-2)^2 + (y-3)^2 = 34$
b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.
Ta có phương trình đường tròn chính giữa:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Tại điểm M(x,y) trên đường tròn, ta có:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:
$y - y_M = y'(x-x_M)$
Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:
$y + 5 = \frac{-(x-1)}{y+5}(x-1)$
Simplifying:
$x(y+5) + y(x-1) = 6$
Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến
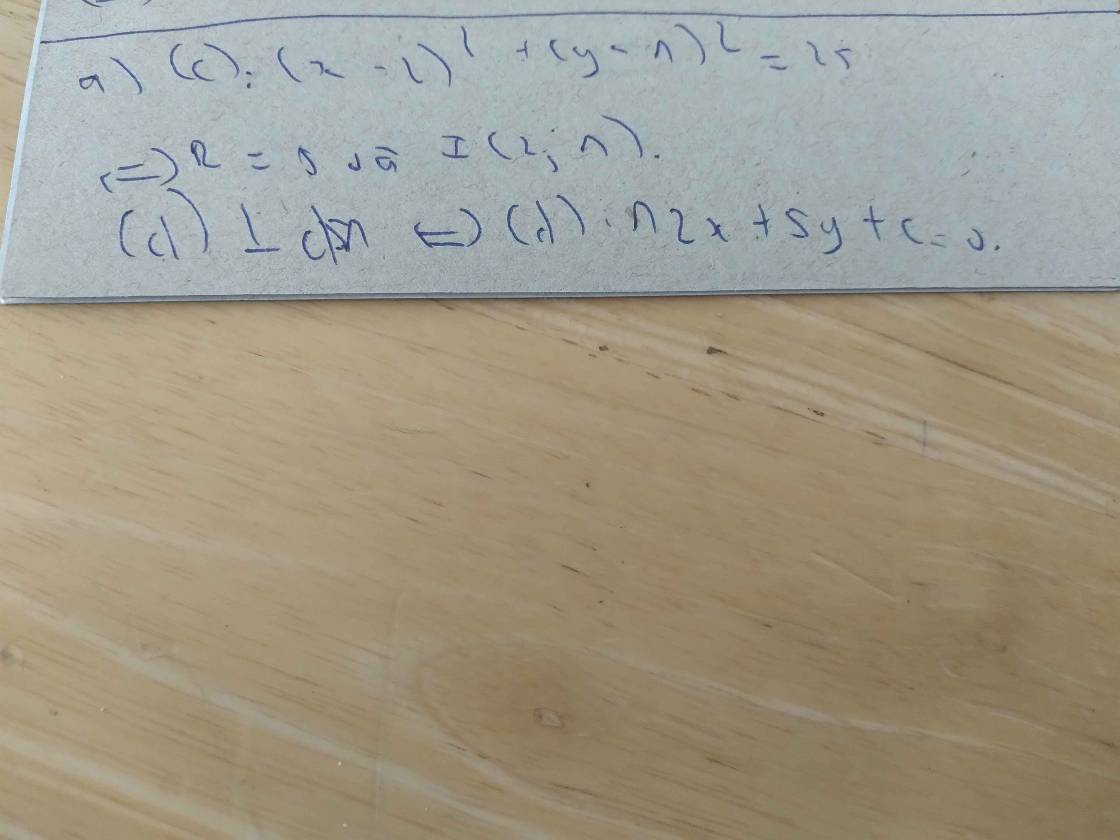

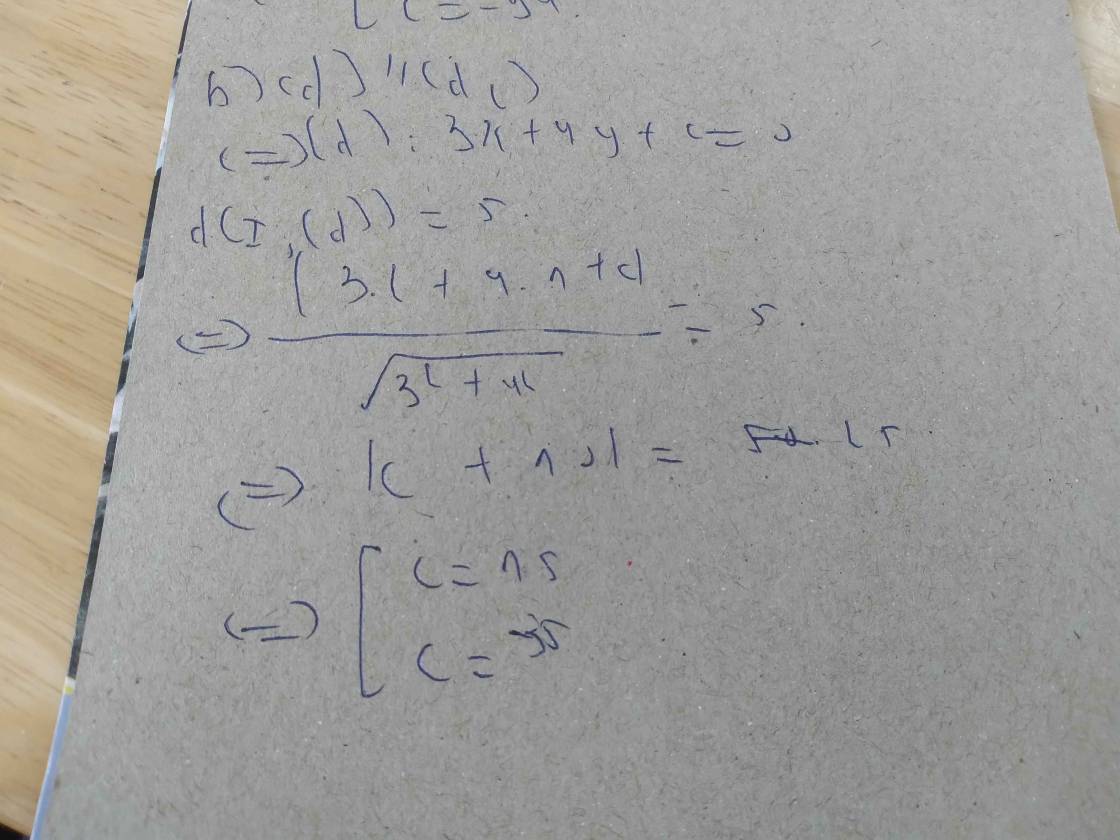
ching chang chong