Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với bức xạ đỏ, λ 1 = 660 nm = 0,66 μm
i 1 = 0,396mm
Với bức xạ lục - vàng, λ 2 = 550 nm = 0,55 μm
i 2 = 0,33mm

Phương pháp:
Sử dụng lí thuyết về bài toán trùng nhau của 2 bức xạ trong giao thoa sóng ánh sáng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Cách giải:
+ Ta có: i1 = 0,6 mm và i2 = 0,78 mm
+ Vị trí hai bức xạ trùng nhau:
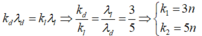

+ Số vân sáng của λ 1 = 500 nm trên đoạn MN là:
![]()
có 10 giá trị
+ Số vân sáng của λ 2 = 650 nm trên đoạn MN là:
![]()
có 8 giá trị
+ Số vân sáng trùng của hai bức xạ trên đoạn MN là:
![]()
có 1 giá trị
+ Số vân sáng quan sát được là: N = N1 + N2 – N0 = 17
Chọn B

Vị trí hai vân sáng trùng nhau thỏa mãn
\(k_1 i_1 = k_2 i_2 \)
<=> \(k_1 \lambda_1 = k_2 \lambda_2\)
<=> \(\frac{k_1}{k_2}= \frac{\lambda_2}{\lambda_1} = \frac{660}{500}= \frac{33}{25}.\)(*)
Vị trí hai vân sáng trùng nhau đầu tiên (trừ vân trung tâm) ứng với \(k_1;k_2\) nhỏ nhất thỏa mãn (*) tức là \(k_1 = 33; k_2 = 25.\)
Thay \(k_1 =33=> \Delta x_{min}= 33.\frac{500.10^{-3}.1,2}{2}=9,9mm.\)
Với \(\lambda = 500nm = 500,10^{-3}\mu m; a = 2mm; D = 1,2m.\)

Chọn C
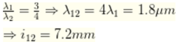
Vậy trên đoạn MN có 3 vị trí vân sáng trùng nhau (7.2, 14.4, 21.6)

Đáp án B
D = 2m, a = 0,5 mm = 0,5.10-3m.
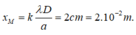
Với 380 nm ≤ λ ≤ 760 nm. Thay vào được 6,57 ≤ k ≤ 13,1 mà k là số nguyên nên ta có kmin = 7 => λ = 0,714µm = 714nm.
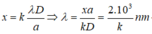
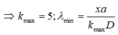
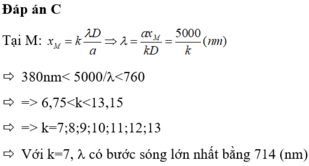
Vân chính giữa ứng với k = 0 là chung cho cả hai bức xạ, tức là tại đó cả hai bức xạ cùng cho vân sáng và vân có màu là màu hỗn hợp của màu đỏ và màu lục, tức là màu vàng - da cam.
Vân đầu tiên cùng màu với vân này ở tại điểm A cách tâm O của vân chính giữa một khoảng X = OA sao cho : x= i 1 k 1 = i 2 k 2 hay là 0,396 k 1 = 0,33 k 2 ;
với k 1 , k 2 là hai số nguyên.
Ta nhận thấy : 6 k 1 = 5 k 2
Vậy giá trị nhỏ nhất của k 1 là 5 và của k 2 là 6, tức là :
OA = 0,396.5 = 0,33.6 = 1,98 mm