Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
? Lời giải:
+ i 2 = λ D 2 a = 750.10 − 6 .2.10 3 2.1 , 5 = 0 , 5 m m

Khoảng cách lớn nhất từ giả thiết nghĩa là khoảng cách từ vân sáng bậc 2 (nửa trên) đến vân tối thứ 4 (nửa dưới)
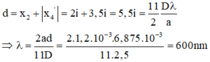
Đáp án D

Vị trí hai vân sáng trùng nhau thỏa mãn
\(k_1 i_1 = k_2 i_2 \)
<=> \(k_1 \lambda_1 = k_2 \lambda_2\)
<=> \(\frac{k_1}{k_2}= \frac{\lambda_2}{\lambda_1} = \frac{660}{500}= \frac{33}{25}.\)(*)
Vị trí hai vân sáng trùng nhau đầu tiên (trừ vân trung tâm) ứng với \(k_1;k_2\) nhỏ nhất thỏa mãn (*) tức là \(k_1 = 33; k_2 = 25.\)
Thay \(k_1 =33=> \Delta x_{min}= 33.\frac{500.10^{-3}.1,2}{2}=9,9mm.\)
Với \(\lambda = 500nm = 500,10^{-3}\mu m; a = 2mm; D = 1,2m.\)

Đáp án C
+ Điều kiện để có sự trùng nhau của hai hệ vân sáng
.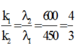
![]()
Xét tỉ số
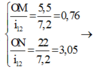 có 3 vân trùng.
có 3 vân trùng.
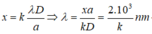
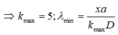
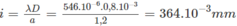

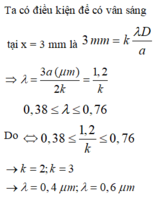
Tại M 1 : x = 1,07mm = 1,07.i/0,364 = 3i
Vậy tại M 1 có vân sáng thứ 3
Tại M 2 : x 2 = 0,91mm = 0,91.i/0,364 = 2,5i = (3 - 1/2)i
Vậy tại M 2 có vân tối thứ 3