Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x,y lần lựợt là số lít nước cam và nước táo cần pha chế.
Số điểm thưởng nhận được là F = 60x + 80y.
Ta có hệ BPT 30 x + 10 y ≤ 210 x + y ≤ 9 x + 4 y ≤ 24 x ≥ 0 ; y ≥ 0 . Miền nghiệm của hệ như hình vẽ.
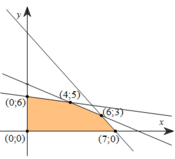
Giá trị lớn nhất của F đạt được tại điểm (4;5). Vậy đội A đã pha chế 4 lít nước cam và 5 lít nước táo.
Đáp án D.

Chọn đáp án C
Phương pháp
- Lập hệ bất phương trình ẩn x, y dựa vào điều kiện đề bài.
- Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.
- Tìm x, y để biểu thức tính số điểm M(x;y) đạt GTLN (tại một trong các điểm mút).
Cách giải
Gọi x, y lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế (x≥0;y≥0)
Để pha chế x lít nước cam thì cần 30x (g) đường, x lít nước và x (g) hương liệu.
Để pha chế y lít nước táo thì cần 10y (g) đường, y lít nước và 4y (g) hương liệu.
Theo bài ra ta có hệ bất phương trình:
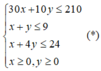
Số điểm đạt được khi pha x lít nước cam và y lít nước táo là: M(x;y)=60x+80y.
Bài toán trở thành tìm x, t thỏa để M(x;y) đạt GTLN.
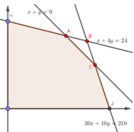
Ta biểu diễn miền nghiệm của (*) trên mặt phẳng tọa độ như sau:
Miền nghiệm là ngũ giác ACJIH
Tọa độ các giao điểm A(4;5),C(6;3),J(7;0),I(0;0),H(0;6).
M(x;y) sẽ đạt max, min tại các điểm đầu mút nên thay tọa độ từng giao điểm vào tính M(x;y) ta được:
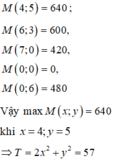

Bài 1 : Giải
Lượng đường trong 1,2kg nước ngọt là: 1,2 x 5 : 100 = 0,06kg
Để có tỉ lệ đường 2,5% thì lượng nước đường là: 0,06 x 100 : 2,5 = 2,4kg
Vậy lượng nước lọc cần đổ thêm là : 2,4 – 1,2 = 1,2 kg
ĐS : 1,2kg
Bài 2 : Giải
Lượng muối trong 1,2kg nước muối là: 1,2 x 3 : 100 = 0,036kg
Để có tỉ lệ muối 2,5% thì lượng nước muối là: 0,036 x 100 : 2,5 = 1,44kg
Vậy lượng nước lọc cần đổ thêm là : 1,44 – 1,2 = 0,24 kg
ĐS : 0,24kg

Chọn B


Vậy để thu được lợi nhuận cao nhất thì cần sản xuất 20 sản phẩm loại I và 40 sản phẩm loại II


Gọi số nước còn lại ở bể 2 là a lít
số nước còn lại ở bể 1 là \(\frac{2}{3}\)a lít
ta có:
Số nước đã chảy ờ bể 1 là : 800-\(\frac{2}{3}\)a ( lít )
Số nước đã chảy ở bể 2 là : 1300-a ( lít)
Thời gian bể 1 đã chảy là : \(\frac{800-\frac{2}{3}a}{15}\) (phút)
Thời gian bể 2 đã chảy là : \(\frac{1300-a}{25}\) (phút)
2 vòi cùng tháo và cùng thời gian chảy => \(\frac{800-\frac{2}{3}a}{15}\)=\(\frac{1300-a}{25}\)
⇔ 20000-\(\frac{50}{3}\)a = 19500-15a
⇔ \(\frac{5}{3}\)a = 500
⇔ a = 300 ( lít)
thời gian để số nước còn lại trong bể thứ nhất bằng 2/3 số nước còn lại trong bể thứ 2 là: t= \(\frac{1300-a}{25}\)= \(\frac{1300-300}{25}\)= 40 (phút)

Đáp án D.
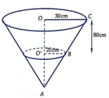
Xét hình nón đỉnh A, đường cao h(h > 80cm) và có đáy là đường tròn tâm O, bán kính R = 30cm. Mặt phẳng cách mặt đáy 80 cm và cắt hình nón theo giao tuyến là đường tròn tâm O' có bán kính r = 20cm. Mặt phẳng chia hình nón thành 2 phần. Phần (I) là phần chứa đỉnh A, phần (II) là phần không chứa đỉnh A (hình vẽ).
Ta có O ' B O C = A O ' A O ⇔ A O ' A O ' + O ' O = 2 3 ⇔ A O ' A O ' + 80 = 2 3 ⇔ A O ' = 160 ( c m )
Thể tích hình nón là V = 1 3 A O . πR 2 = 1 3 160 + 80 . π . 30 2 = 72000 π ( cm 3 )
Thể tích phần (I) là V I = 1 3 A O ' . πr 2 = 1 3 160 π . 20 2 = 64000 3 π ( cm 3 )
Thể tích cái xô cũng là thể tích phần (II), ta có :
V ( I I ) = V - V ( I ) = 72000 π - 64000 3 π = 152000 3 π ( cm 3 ) = 19 375 π ( m 3 )
Vậy số tiền phải trả mỗi tháng là
20000 . V I I . 10 = 20000 . 19 375 π . 10 ≈ 31835 (đồng).

Chọn đáp án C
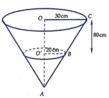
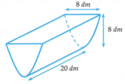
Xét mặt cắt là một hình parabol, chọn hệ trục tọa độ như hình vẽ bên.
Phương trình parabol (P) có dạng y = a x 2 với a > 0 .
Ta thấy (P) đi qua các điểm (-4; 8) và (4; 8) nên a = 1 2 .
Suy ra phương trình parabol (P) là y = 1 2 x 2
Diện tích mặt cắt parabol của bồn nước cùng chính là diện tích của hình phẳng được giới hạn bởi các đường y = 1 2 x 2 và y = 8.
Diện tích đó là:
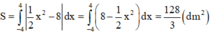
Do đó thể tích của bồn nước là: V = 2560 3 d m 3

đổi 12dm=1,2m
Thể tích của bể là: 3 x 2 x 1,2 = 7,3 ( m3 )
Trong bể có số lít nước là: 7,3 : 100 x 75 = 5, 475 ( m3) = 5475 lít nước
Số lít nước để bể đầy là 7,3 ( m3) = 7300 lít nước
Số lít nước phải đổ thêm để đầy bể là 7300 - 5475 =1835 (l)
vậy số nước cần đổ thêm để dầy bình là 1835 lít nước
Chọn C.
Gọi số lít nước ngọt loại I là x và số lít nước ngọt loại II là y. Khi đó ta có hệ điều kiện về vật liệu ban đầu mà mỗi loại được cung cấp: