Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(x-x0)^2+(y-y0)^2=R^2
I(x;x-6)
=> (x-6)^2+(x-6-4)^2=R^2
(x-4)^2+(x-6)^2=R^2
=> x^2-12x+36+x^2-20x+100=x^2-8x+16+x^2-12x+36
=>12x=84
=>x=7
=>R^2=10
`=>(7-x0)^2+(1-y0)^2=10`

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
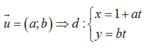
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
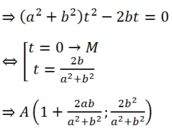
- Nếu d cắt (C2) tại B:
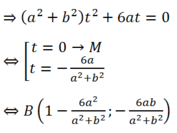
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
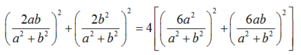
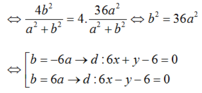

Đường tròn \((C)\) tâm \(I(a;b)\) bán kính \(R\)có phương trình
\((x-a)^2+(y-b)^2=R^2.\)
\(∆MAB ⊥ M\) \(\rightarrow \) \(AB\) là đường kính suy ra \(∆\) qua \(I\) do đó:
\(a-b+1=0 (1)\)
Hạ \(MH⊥AB\) có \(MH=d(M, ∆)= \dfrac{|2-1+1|}{\sqrt{2}}={\sqrt{2}} \)
\(S_{ΔMAB}=\dfrac{1}{2}MH×AB \Leftrightarrow 2=\dfrac{1}{2}2R\sqrt{2} \)
\(\Rightarrow R = \sqrt{2} \)
Vì đường tròn qua\(M\) nên (\(2-a)^2+(1-b)^2=2 (2)\)
Ta có hệ :
\(\begin{cases} a-b+1=0\\ (2-a)^2+(1-b)^2=0 \end{cases} \)
Giải hệ \(PT\) ta được: \(a=1;b=2\).
\(\rightarrow \)Vậy \((C) \)có phương trình:\((x-1)^2+(y-2)^2=2\)