Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

Bài 2:
a: \(R=d\left(I;d\right)=\dfrac{\left|-2\cdot3+1\cdot\left(-4\right)\right|}{\sqrt{3^2+\left(-4\right)^2}}=2\)
Phương trình (C) là:
(x+2)^2+(y-1)^2=2^2=4
Bài 1:
a: I thuộc Δ nên I(x;-2x-3)
IA=IB
=>IA^2=IB^2
=>\(\left(x+5\right)^2+\left(-2x-3-1\right)^2=\left(x+2\right)^2+\left(-2x-3-4\right)^2\)
=>x^2+10x+25+4x^2+16x+16=x^2+4x+4+4x^2+28x+49
=>26x+41=32x+53
=>-6x=-12
=>x=2
=>I(2;-7): R=IA=căn 113
Phương trình (C) là:
(x-2)^2+(y+7)^2=113
2: vecto IA=(7;-8)
Phương trình tiếp tuyến là:
7(x+5)+(-8)(y-1)=0
=>7x+35-8y+8=0
=>7x-8y+43=0

1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0

a.
Gọi phương trình đường tròn (C) có dạng:
\(x^2+y^2-ax-by+c=0\)
Do A;B;C thuộc (C) nên: \(\left\{{}\begin{matrix}0+16-0.a-4b+c=0\\9+16-3a-4b+c=0\\9+0-3a-0.b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4b+c=-16\\-3a-4b+c=-25\\-3a+c=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=4\\c=0\end{matrix}\right.\)
Hay pt (C) có dạng: \(x^2+y^2-3x-4y=0\)
b.
Đường tròn (C) tiếp xúc (d) nên có bán kính \(R=d\left(C;d\right)=\dfrac{\left|3.3+0.4-5\right|}{\sqrt{3^2+4^2}}=\dfrac{4}{5}\)
Phương trình: \(\left(x-3\right)^2+y^2=\dfrac{16}{25}\)

1: Gọi I(0,y) là tâm cần tìm
Theo đề, ta có: IA=IB
=>\(\left(0-3\right)^2+\left(5-y\right)^2=\left(1-0\right)^2+\left(-7-y\right)^2\)
=>y^2-10y+25+9=y^2+14y+49+1
=>-10y+34=14y+50
=>-4y=16
=>y=-4
=>I(0;-4)
=>(x-0)^2+(y+4)^2=IA^2=90
2: Gọi (d1) là đường thẳng cần tìm
Vì (d1)//(d) nên (d1): 4x+3y+c=0
Theo đề, ta có: d(I;(d1))=3 căn 10
=>\(\dfrac{\left|0\cdot4+\left(-4\right)\cdot3+c\right|}{5}=3\sqrt{10}\)
=>|c-12|=15căn 10
=>\(\left[{}\begin{matrix}c=15\sqrt{10}+12\\c=-15\sqrt{10}+12\end{matrix}\right.\)
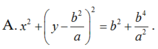
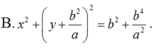
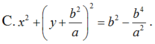
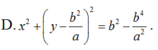

Đáp án B
Do đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C
Nên tam giác ABC cân tại A
tâm I của (C) thuộc Oy nên I(0; y0)
Do:
Mặc khác:
Vậy phương trình của là: