Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số 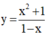 có đồ thị hàm số như sau:
có đồ thị hàm số như sau:
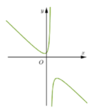 õ ràng
õ ràng ![]()
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số ![]() => Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là:
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: ![]() luôn song song với trục hoành.
luôn song song với trục hoành.
Vậy (III) đúng.

Đáp án A
Phương pháp:
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau ![]()
Cách giải: 
Gọi 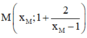
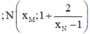 là hai điểm thuộc đồ thị hàm số.
là hai điểm thuộc đồ thị hàm số.
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau
![]()
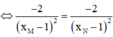
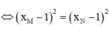
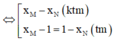
![]()
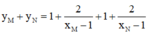
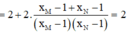
Gọi I là trung điểm của MN ta có: I(1;1)
Dễ thấy đồ thị hàm số có TCN là y = 1 và tiệm cận đứng x = 1 → I(1;1) là giao điểm của hai đường tiệm cận => C đúng.
TCN y = 1 và tiệm cận đứng x = 1 rõ ràng đi qua trung điểm I của đoạn MN=> B, D đúng

Đáp án B
Ta có: y ' = 3 x 2 + 6 m x + m + 1 ⇒ y ' - 1 = 4 - 5 m ; y - 1 = 2 m - 1
PTTT tại điểm có hoành độ x 0 = - 1 là y = 4 - 5 m x + 1 + 2 m - 1
Do tiếp tuyến qua A 1 ; 3 ⇒ 3 = 2 4 - 5 m + 2 m - 1 ⇔ - 4 = - 8 m ⇔ m = m 0 = 1 2 .


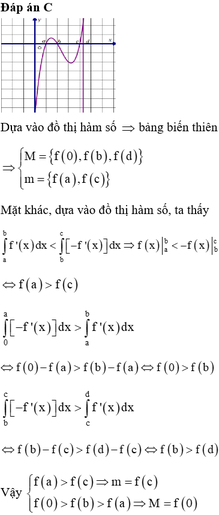
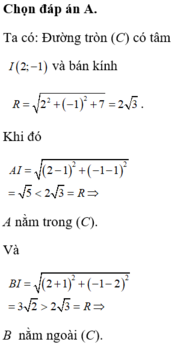
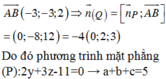

Chọn D