Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\widehat{AIB}=90^0\Rightarrow\widehat{ACB}=45^0\) hoặc \(\widehat{ACB}=135^0\Rightarrow\widehat{ACD}=45^0\Rightarrow\Delta ACD\) vuông cân tại D nên DA=DC
Hơn nữa IA=IC => \(DI\perp AC\Rightarrow\) đường thẳng AC thỏa mãn điều kiện AC qua điểm M và AC vuông góc ID.
Viết phương trình đường thẳng AC : \(x-2y+9=0\)
Gọi \(A\left(2a-9;a\right)\in AC\). Do \(DA=\sqrt{2}d\left(D,AC\right)=2\sqrt{10}\) nên
\(\sqrt{\left(2a-8\right)^2+\left(a+1\right)^2}=2\sqrt{10}\Leftrightarrow a^2-6a+5=0\)
\(\Leftrightarrow\begin{cases}a=1\Rightarrow A\left(-7;1\right)\\a=5\Rightarrow A\left(1;5\right)\end{cases}\)
Theo giả thiết đầu bài \(\Rightarrow A\left(1;5\right)\)
Viết phương trình đường thẳng DB : \(x+3y+4=0\). Gọi \(B\left(-3b-4;b\right)\)
Tam giác IAB vuông tại I nên : \(\overrightarrow{IA.}\overrightarrow{IB}=0\Leftrightarrow3\left(-3b-2\right)+4\left(b-1\right)=0\Leftrightarrow b=-2\Rightarrow B\left(2;-2\right)\)
Đáp số \(A\left(1;5\right);B\left(2;-2\right)\)

gọi K1 là giao điểm của AK với BC. Đầu tiên e chứng minh I là trực tâm của Tam Giác AK1B.
chứng minh tam giác AK1B cân tại K1, rồi suy ra K1M vuông góc vowis AB, suy ra I là trực tâm. rồi e làm như bình thường

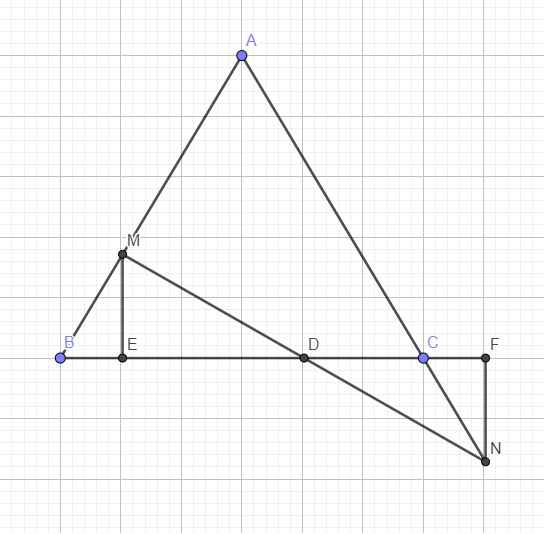
Gọi D là giao điểm MN và BC
Từ M kẻ ME vuông góc BC, từ N kẻ NF vuông góc BC
\(\widehat{B}=\widehat{C}=\widehat{NCF}\Rightarrow\Delta MBE=\Delta NCF\left(ch-gn\right)\)
\(\Rightarrow ME=NF\)
\(\Rightarrow\Delta MED=\Delta NFD\)
\(\Rightarrow MD=ND\) hay D là trung điểm MN
\(\Rightarrow D\left(-1;3\right)\Rightarrow\overrightarrow{ED}=\left(2;4\right)=2\left(1;2\right)\)
Phương trình BC (hay ED) có dạng:
\(2\left(x+3\right)-1\left(y+1\right)=0\Leftrightarrow2x-y+5=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+4=0\\2x-y+5=0\end{matrix}\right.\) \(\Rightarrow B\left(-4;-3\right)\)
\(\Rightarrow\overrightarrow{BM}=\left(3;4\right)\) \(\Rightarrow cosB=\dfrac{\left|3.1+4.2\right|}{\sqrt{3^2+4^2}.\sqrt{1^2+2^2}}=\dfrac{11\sqrt[]{5}}{25}\)
Do C thuộc BC nên tọa độ dạng: \(C\left(c;2c+5\right)\Rightarrow\overrightarrow{NC}=\left(c+1;2c+12\right)\)
\(cosC=cosB=\dfrac{11\sqrt{5}}{25}=\dfrac{\left|1.\left(c+1\right)+2\left(2c+12\right)\right|}{\sqrt{1^2+2^2}.\sqrt{\left(c+1\right)^2+\left(2c+12\right)^2}}\)
\(\Leftrightarrow c^2+10c-96=0\Rightarrow\left[{}\begin{matrix}c=6\Rightarrow C\left(6;17\right)\\c=-16\Rightarrow C\left(-16;-27\right)\end{matrix}\right.\)
(Loại \(C\left(-16;-27\right)\) do D nằm giữa B và C)
Viết phương trình AB (qua M và B), viết phương trình AC (qua N và C). Tọa độ A là giao AB và AC