Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(I=AM\cap BN\), \(\Delta BIM\) đồng dạng \(\Delta ABM\)
suy ra \(AM\perp BN\) nên \(BN:-2x-y+c=0\)
\(N\left(0;-2\right)\Rightarrow c=-2\Rightarrow BN:2x-y-2=0\)
Tọa độ điểm I là nghiệm hệ phương trình :
\(\begin{cases}x+2y-2=0\\2x-y-2=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=\frac{6}{5}\\y=\frac{2}{5}\end{cases}\) \(\Rightarrow I\left(\frac{6}{5};\frac{2}{5}\right)\)
Từ \(\Delta ABM\) vuông : \(BI=\frac{AB.BM}{\sqrt{AB^2+BM^2}}=\frac{4}{\sqrt{5}}\)
Tọa độ điểm \(B\left(x;y\right)\) thỏa mãn \(\begin{cases}B\in BN\\BI=\frac{4}{\sqrt{5}}\end{cases}\) \(\Rightarrow\begin{cases}2x-y-2=0\\\left(\frac{6}{5}-x\right)^2+\left(\frac{2}{5}-y\right)^2=\frac{16}{5}\end{cases}\)
Giải hệ ta được \(\begin{cases}x=2\\y=2\end{cases}\) và \(\begin{cases}x=\frac{2}{5}\\y=\frac{-6}{5}\end{cases}\) Suy ra \(B\left(2;2\right)\) Loại \(\left(\frac{2}{5};-\frac{6}{5}\right)\)
Tọa đọ M(x;y) thỏa mãn \(\begin{cases}M\in AM\\IM=\sqrt{BM^2-BI^2}\end{cases}\) \(\Rightarrow\begin{cases}x+2y-2=0\\\left(x-\frac{6}{5}\right)^2+\left(y-\frac{2}{5}\right)^2=\frac{4}{5}\end{cases}\)
Giải hệ ta được : \(\begin{cases}x=2\\y=0\end{cases}\) và \(\begin{cases}x=\frac{2}{5}\\y=\frac{4}{5}\end{cases}\) suy ra \(M_1\left(2;0\right);M_2\left(\frac{2}{5};\frac{4}{5}\right)\)

Đáp án D
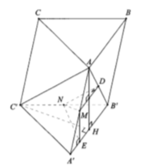
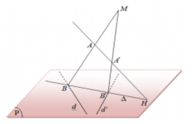
Ta có d đi qua N(2;5;2) chỉ phương u d → = ( 1 ; 2 ; 1 ) đi qua N'(2;1;2) chỉ phương u d ' → = ( 1 ; - 2 ; 1 )
Gọi (R) là mặt phẳng chứa A và d, gọi (Q) là mặt phẳng chứa A¢ và d¢
Từ giả thiết ta nhận thấy điểm M nằm trong các mặt phẳng (R), (Q) nên đường thẳng cố định chứa M chính là giao tuyến của các mặt phẳng (R), (Q).
Vậy (R) đi qua N(2;5;2) có cặp chỉ phương là u d → = ( 1 ; 2 ; 1 ) , u → = ( 15 ; - 10 ; - 1 )
![]()
(R) đi qua A(a;0;0) => a=2
Tương tự (Q) đi qua N'(2;1;2) có cặp chỉ phương u d → = ( 1 ; 2 ; 1 ) , u → = ( 15 ; - 10 ; - 1 )
![]()
(Q) đi qua B(0;0;b) => b=4
Vậy T = a+b=6





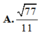


=>x^3-3*x^2*1+3*x*1-1^3-27=0
=>(x-1)^3 -27 =0
=> (x-1)^3=27
=>x-1=3
=> x=4
Vậy chọn A
a