Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{i}=\left(1;1\right)\) nên tồn tại một số thực t sao cho \(\overrightarrow{u}=t.\overrightarrow{i}\) ⇒ \(\overrightarrow{u}=\left(t;t\right)\)
d : 3x - y - 7 = 0 nên A (2 ; - 1) ∈ d
Sau khi thực hiện phép tịnh tiến thì ta được điểm B trên d; : 3x - y + 13
thỏa mãn \(\overrightarrow{AB}=\overrightarrow{u}=\left(t;t\right)\)
⇒ B (t + 2 ; t - 1)
Do B ∉ d' ⇒ 3(t + 2) - (t - 1) + 13 = 0
⇒ t = - 10
⇒ Vecto tịnh tiến là \(\overrightarrow{u}=\left(-10;-10\right)\)

Thực hiện phép đối xứng tâm O biến d thành d’, sau đó thực hiện phép tịnh tiến theo u → biến d’ thành đường thẳng d”.
* Qua phép đối xứng tâm O: biến điểm M(x; y) thuộc d thành điểm M’(x’; y’) thuộc d’.
Ta có: x ' = − x y ' = − y ⇔ x = − x ' y = − y ' Vì M thuộc d nên: x+ y – 2 = 0 . Suy ra:
-x’ + (- y’) – 2 = 0 hay x’+ y’ + 2= 0
Phương trình đường thẳng d’ : x + y + 2 = 0
* Qua phép đối xứng tịnh tiến theo ( 3; 2) biến điểm A(x; y) thuộc đường thẳng d’ thành điểm A’ (x’; y’) thuộc đường thẳng d”. Ta có:
A A ' → = u → ⇔ x ' − x = 3 y ' − y = 2 ⇔ x = x ' − 3 y = y ' − 2
Vì điểm A thuộc đường thẳng d’ nên: x+ y + 2 =0
Suy ra: (x’ - 3) + (y’ - 2) + 2 = 0 hay x’ + y’ - 3 = 0
Phương trình đường thẳng d” là x + y – 3 = 0
Đáp án D

Lấy M(x; y) thuộc d; gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto v → ( 1 ; 0 ) thì
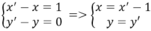
Thay vào phương trình d ta được x’ – 2 = 0, hay phương trình d’ là x – 2 = 0.
Đáp án B

Gọi vecto tịnh tiến có dạng \(\overrightarrow{v}=\left(a;0\right)\)
\(M\left(0;-1\right)\) là 1 điểm thuộc d
M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=0+a=a\\y_{M'}=-1+0=-1\end{matrix}\right.\) \(\Rightarrow M'\left(a;-1\right)\)
Thay vào pt d':
\(a-1-1=0\Leftrightarrow a=2\)
Vậy \(\overrightarrow{v}=\left(2;0\right)\)
thầy ơi cho em hỏi vì sao vecto v lại biết đc số 0 là y v thầy

Đáp án A
Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là u d → = ( 1 ; 2 )