Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta có:
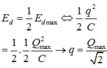
+ Vậy góc quét được trong thời gian trên là φ = π 4
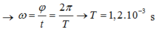
+ Góc quét khi điện tích giảm từ Q m a x còn Q m a x 2 là φ = π 3
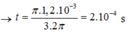

Thời gian ngắn nhất để năng lượng điện trường giảm từ giá trị cực đại xuống còn 1 nửa giá trị cực đại là
\(t = \frac{\varphi}{\omega}=\frac{\pi/3}{2\pi/T} = \frac{T}{6}.\)
Như vậy suy luận của bạn bị nhầm. Ban đầu \(\frac{T}{6} = 1,5.10^{-4}s.\) Đây chính là chu kì dao động của Wc.
Sau đó bạn biện luận chính xác là muốn tính chu kì của q là T' = 2T.

Đáp án D
+ Ta có:
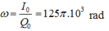
+ Thời gian ngắn nhất để điện tích giảm từ giá trị cực đại đến nửa giá trị cực đại tương ứng với góc quét được là ∆ φ = π 3
![]()

Đáp án D
+ Tần số góc của dao động: 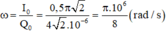
+ Chu kì dao động của mạch: 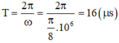
+ Thời gian ngắn nhất để diện tích trên tụ giảm từ giá trị cực đại xuống còn một nửa giá trị là
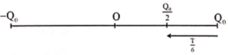
![]()

Đáp án A
Chu kì của mạch dao động LC là 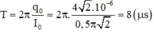
Khoảng thời gian ngắn nhất để điện tích trên bản tụ giảm từ giá trị cực đại đên một nửa giá trị cực đại là: ![]()

Đáp án C
+ Khoảng thời gian ngắn nhất để dòng điện giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là Δ t = T 6 = 800 μ s → T = 4800 μ s
+ Năng lượng từ trường trong mạch giảm từ cực đại đến còn một nửa trong khoảng thời gian Δ t = 0 , 125 T = 600 μ s

Đáp án D
Khoảng thời gian ngắn nhất để cường độ dòng điện qua cuộn cảm giảm từ độ lớn cực đại xuống còn một nửa độ lớn cực đại là T 6 còn khoảng thời gian ngắn nhất để năng lượng từ trường trong mạch giảm từ độ lớn cực đại xuống còn một nửa giá trị cực đại là T 8


Chọn đáp án C
Gọi chu kì dao động của mạch là T thì thời gian ngắn nhất để năng lượng điện trường đang có giá trị cực đại giảm đi một nửa là t = T/8 = 1,5.10−4s → T = 1,2. 10−4s.
Thời gian ngắn nhất để điện tích trên tụ đang có giá trị cực đại giảm còn một nửa:
t’ = T/6 = 2. 10−4s