Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
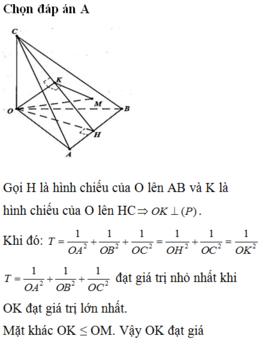
Vì OA, OB, OC đôi một vuông góc và M là trực tâm tam giác ABC => OM ⊥ (ABC)
Suy ra mp(ABC) nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình mp(P):
![]()
<=> x +2y+3z -14=0

Chọn D
Gọi A (a;0;0), B (0;b;0), C (0;0;c), do A, B, C thuộc ba tia Ox, Oy, Oz nên a, b, c > 0.


Chọn D
Giả sử A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c > 0
Khi đó mặt phẳng (P) có dạng ![]() .
.
Vì (P) đi qua M nên 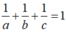
Mặt khác OA = 2OB nên a = 2b nên ![]()
Thể tích khối tứ diện OABC là: V= abc/6
Ta có:
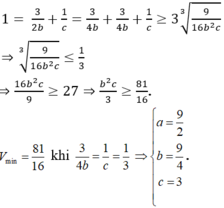

Đáp án C
Phương pháp
+) Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) viết phương trình mặt phẳng (P) đi qua A, B, C dạng đoạn chắn.M ∈ (P)=> Thay tọa độ điểm M vào phương trình mặt phẳng (P).
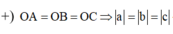
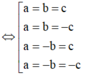
+) Ứng với mỗi trường hợp tìm các ẩn a, b, c tương ứng
Cách giải
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) khi đó phương trình mặt phẳng đi qua A, B, C là
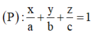
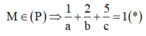
![]()
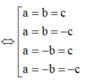
TH1: a=b=c thay vào (*) có
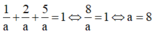
![]()
TH2: a=b=-c thay vào (*) có
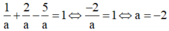
![]()
TH3: a=-b=c thay vào (*) có
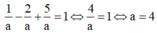
![]()
TH4: a=-b=-c thay vào (*) có
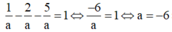
![]()
Vậy có 4 mặt phẳng thỏa mãn.