Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi C là trung điểm của AB ⇒ C(0;1;-1) ⇒ phương trình đường thẳng qua C và song song với AB là: x 1 = y - 1 - 1 = z + 1 2

Đáp án A
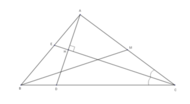
Gọi M là trung điểm của AC, E là chân đường phân giác trong góc C. Ta có:
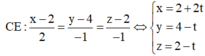
![]()

Vì M thuộc đường trung tuyến kẻ từ B có phương trình
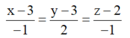
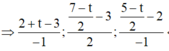
![]()
Kẻ AH vuông góc với CE tại H, cắt BC tại D => Tam giác ACD cân tại C vậy H là trung điểm của AD.
![]()
![]()
vectơ chỉ phương của CE là u → 1 =(2;-1;-1)
![]()
![]()
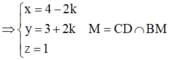
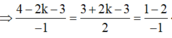
![]()
A B → =(0;2;-2). u → =(m;n;-1) là một vectơ chỉ phương của AB
=> A B → và u → cùng phương.
![]()
![]()

Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là ![]() , a²+b²+c²>0.
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
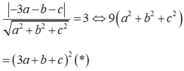
Thay 3a=2 (c+b ) vào (*) ta được:
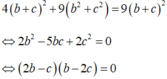
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))

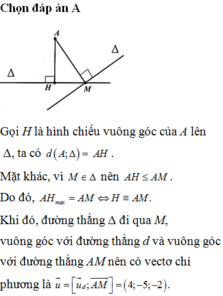
Chọn C
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.

Phương trình tham số d: \(\left\{{}\begin{matrix}x=t\\y=-1+2t\\z=2+3t\end{matrix}\right.\) \(\Rightarrow\overrightarrow{u_d}=\left(1;2;3\right)\)
Gọi A là giao điểm \(d\) và (P) \(\Rightarrow\) tọa độ A thỏa mãn:
\(t-1+2t+2+3t-3=0\Rightarrow t=\frac{1}{3}\Rightarrow A\left(\frac{1}{3};-\frac{1}{3};3\right)\)
Gọi (Q) là mặt phẳng chứa d và vuông góc (P) \(\Rightarrow\left(Q\right)\) có 1 vtpt là:
\(\Rightarrow\overrightarrow{n_{\left(Q\right)}}=\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{u_d}\right]=\left(1;-2;1\right)\)
Gọi \(d'\) là hình chiếu của \(d\) lên (P)
\(\left[\overrightarrow{n_{\left(p\right)}};\overrightarrow{n_{\left(Q\right)}}\right]=\left(3;0;-3\right)\) \(\Rightarrow d'\) nhận \(\overrightarrow{u_{d'}}=\left(1;0;-1\right)\) là 1 vtcp
Phương trình tham số d': \(\left\{{}\begin{matrix}x=\frac{1}{3}+t\\y=-\frac{1}{3}\\z=3-t\end{matrix}\right.\)

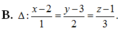


Đáp án B