Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
Ta có đường thẳng MM’ đi qua M, vecto chỉ phương
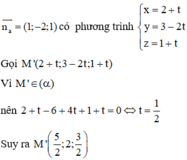
Ta có 
mặt phẳng (P) có VTPT 
Suy ra 
Mặt phẳng
α
đi qua P(2;0;-1) và nhận 
làm một VTPT nên có phương trình
α
: -7x + 11y + z + 15 = 0
Chọn C.
Đáp án B
Phương pháp:
Hình chiếu của điểm M(x0;y0;z0) trên trục Ox là điểm M1(x0;0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oy là điểm M2(0;y0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oz là điểm M3(0;0;z0)
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c), (a,b,c ≠ 0) là: x a + y b + z c = 1
Cách giải: Hình chiếu của điểm A(2; –1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0; –1;0), (0;0;1)
Phương trình mặt phẳng (α): x 2 + y - 1 + z 1 = 1
Chọn D.
Ta có (P) qua O(0;0;0) và nhận BA → = ( 1 ; 3 ; - 5 ) là một VTPT
⇒ ( P ) : x + 3 y - 5 z = 0 .
Đáp án B
Phương pháp giải: Viết phương trình đường thẳng vuông góc với mặt và đi qua điểm, tọa độ giao điểm của đường thẳng và mặt phẳng chính là tọa độ hình chiếu của điểm
Lời giải:
Gọi H là hình chiếu của A trên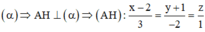
Vì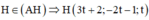
mà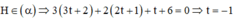
Vậy tọa độ điểm cần tìm là H (–1;1;–1)