Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Mặt cầu (S) tâm I(2;-1;-2) và bán kính R =2. Để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung thì

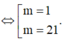

Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là ![]() , a²+b²+c²>0.
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
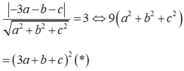
Thay 3a=2 (c+b ) vào (*) ta được:
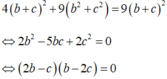
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))

Đáp án D
Phương pháp: AB lớn nhất
![]()
Cách giải: Mặt cầu (S) có tâm I(0;-2;0) và bán kính R = 5
![]()
Ta có
![]()
![]()
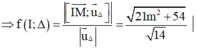
Để AB lớn nhất
![]()

Chọn C
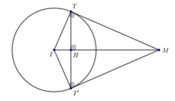
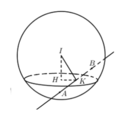
Mặt cầu (S) có tâm I(1;2;3), bán kính R =2. Mặt phẳng (ITT') cắt d tại điểm M (như hình vẽ trên). Gọi H là giao điểm của TT' và MI.
![]()
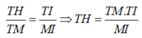
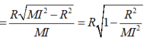
Do TT' = 2TH nên
![]()
Nhận xét rằng với
![]()
![]()
nên khi thay đổi ta luôn có
![]()
cố định. Vì thế
![]()
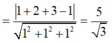
Từ đó ta có:
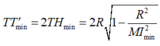
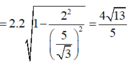
Ta kiểm tra điều kiện đủ của bài toán, tức là chứng minh rằng hình chiếu vuông góc của I lên (P) thuộc vào đường thẳng d.
Gọi d' là đường thẳng qua I và vuông góc với ta có:
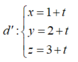
Gọi M là hình chiếu vuông góc của I lên (P) ta có:
![]()
![]()
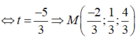
Xét hệ
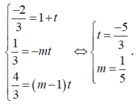
Vậy với m = 1 5 thì độ dài của TT' nhỏ nhất.


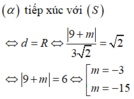
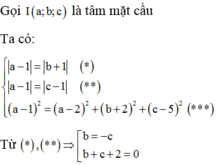
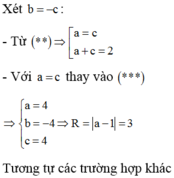
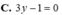

Chọn D