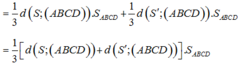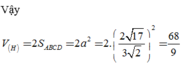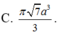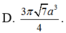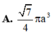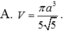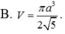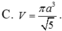Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
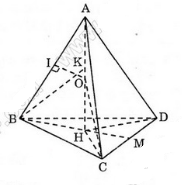
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
![]()
![]()
Từ đó ta có:
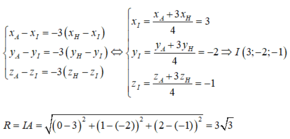
Vậy đáp án C đúng.

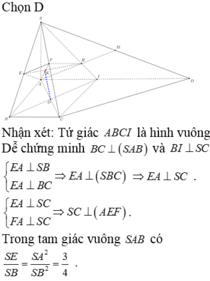
Đáp án D
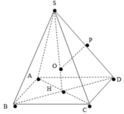
Do AB // CD nên mặt phẳng (ABM) cắt mặt phẳng (SCD) theo một giao tuyến đi qua M và song song với CD, giao tuyến đó cắt SD tại N. Suy ra N là trung điểm của SD. Từ giả thiết ta có:
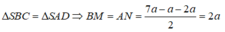
Áp dụng công thức đường trung tuyến trong tam giác SBC ta có:
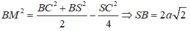
Khối nón đã cho có:
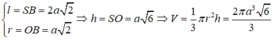

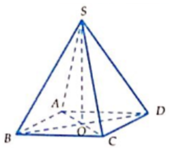
Đáp án C.
* Hướng dẫn giải:
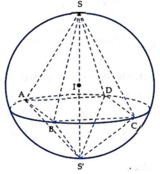
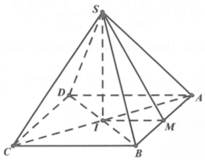
Gọi H = A C ∩ B C , hình chóp tứ giác đều S.ABCD
⇒ S H ⊥ ( A B C D )
Dựng hình như bên với OP là đường trung trực của đoạn SD
⇒ SO = OA = OB = OC = OD = R
![]()
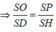
⇒ R = S O = S D . S P S H = S D 2 2 . S H
![]()
![]()
Cạnh AC = 2a ⇒ A H = a ⇒ S H = a 3
![]()
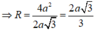

![]()
Diện tích xung quanh của hình trụ là:
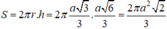
Thể tích của khối trụ là;
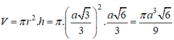

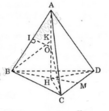
a,+) Từ A vẽ AH _|_ (BCD) (theo giả thiết AB = AC = AD)
Nên \(\Delta ABH=\Delta ACH=\Delta ADH\)
=> HB = HC = HD
Vậy H là tâm đường tròn ngoại tiếp tam giác BCD
+) Ta có: \(AH=\sqrt{AB^2-BH^2}\) với \(BH=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{3a^2}{9}}=\dfrac{a\sqrt{6}}{3}\)
b, Ta có: \(H=AH=\dfrac{a\sqrt{6}}{3};r=BH=\dfrac{a\sqrt{3}}{3}\)
Diện tích xung quanh hình trụ là:
\(S_{xq}=2\pi rh=2\pi.\dfrac{a\sqrt{3}}{3}.\dfrac{a\sqrt{6}}{3}=\dfrac{2\pi\pi^2\sqrt{2}}{3}\)
Thể tích khối trụ là:
\(V=\pi r^2h=\pi\left(\dfrac{a\sqrt{3}}{3}\right)^2.\dfrac{a\sqrt{6}}{3}=\dfrac{\pi a^3\sqrt{6}}{9}\)