Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Phương pháp:
Đường thẳng
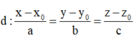
có 1 VTCP là u 1 → =(a;b;c). Mọi vectơ v → =k u → (k ∈ Z)cùng phương với vecto u → đều là VTCP của đường thẳng d.
Cách giải: Đường thẳng d nhận u → =(1;-1;1) là 1 VTCP. Mọi vecto cùng phương với vecto đều là VTCP của đường thẳng d.
Ta thấychỉ có đáp án D, vecto u 1 → =(1;1;1) không cùng phương với u → =(1;-1;1) nên u 1 → =(1;1;1) không là VTCP của đường thẳng d.
Đáp án C
Mặt phẳng (P) có một véc-tơ pháp tuyến là 
=(4;0;-1),
do đường thẳng 
, nên véc-tơ pháp tuyến của mặt phẳng (P) cũng là véc-tơ chỉ phương của đường thẳng d.
Đáp án B
Ta có 
=(2;3;4). Suy ra véc-tơ 
=(2;3;4) là một véc-tơ chỉ phương của đường thẳng AB.
Đáp án B
vuông góc 
thì d có thể nằm trong (P).
d song song (P) thì 
vuông góc 
.
d vuông góc (P) thì 
cùng phương 
.
là một véc-tơ chỉ phương của đường thẳng AB.
. Véc-tơ nào sau đây là một véc-tơ chỉ phương của d?
=(-1;3;2)
=(2;-1;3)
=(-1;3;2).
. Véc-tơ chỉ phương 
