Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình mặt phẳng (ABC) là x 3 + y 2 + z 6 = 1 →2x+3y+z-6=0
Dễ thấy D ϵ (ABC). Gọi H,K,I lần lượt là hình chiếu của A,B,C trên ∆.
Do ∆ là đường thẳng đi qua D nên AH≤ AD,BK≤ BD,CI≤ CD.
Vậy để khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất thì ∆ là đường thẳng đi qua D và vuông góc với (ABC). Vậy phương trình đường thẳng ∆ là x = 1 + 2 t y = 1 + 3 t ( t ∈ ℝ ) z = 1 + t . Kiểm tra ta thấy điểm M(5;7;3) ϵ ∆
Đáp án A

Đáp án B.
Ta thấy D ∈ ( A B C ) : 2 x + 3 y + z = 0
Ta có: d A , d ≤ A D d B , d ≤ B D d C , d ≤ C D ⇒ d A , d + d B , d + d C , d ≤ A D + B D + C D
Dấu “=” xảy ra khi d ⊥ A B C tại điểm D ⇒ d : x = 1 + 2 t y = 1 + 3 t z = z + t ⇒ N 5 ; 7 ; 3 ∈ d


- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
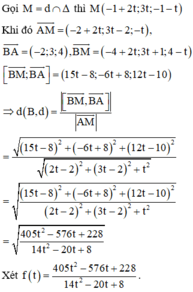
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)


Đáp án D
Điểm A ( 2 ; 1 ; − 3 ) , B ( 2 ; 4 ; 1 ) , O 0 ; 0 ; 0 suy ra G là trọng tâm tam giác ABO là G 2 3 ; 5 3 ; − 2 3
Gọi M, N, P lần lượt là hình chiếu vuống góc cuả A, B, O trên đường thẳng d
Khi đó, khoảng cách:
d A → d = A M ; d B → d = B N ; d O → d = O P
Mặt khác A M ≤ A G B N ≤ B G O P ≤ O G
⇒ d A → d + d B → d + d O → d ≤ A G + B G + O G = c o n s t
Dấu “=” xảy ra khi và chỉ khi đường thẳng d vuông góc mặt phẳng A B O tại G
Ta có O A → = 2 ; 1 ; − 3 O B → = 2 ; 4 ; 1 ⇒ n A B O → = 13 ; − 8 ; 6
⇒ véc tơ chỉ phương của (d) là u → = − 13 ; 8 ; − 6


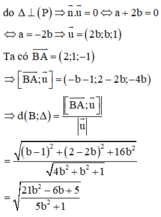

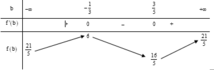
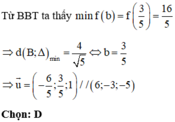
Chú ý khi giải: Các em có thể tham khảo cách 2:
+) Lập phương trình mặt phẳng (Q) đi qua A và song song với (P).
+) Khi đó Δ cần tìm là một đường thẳng nằm trong (Q) và đi qua A.

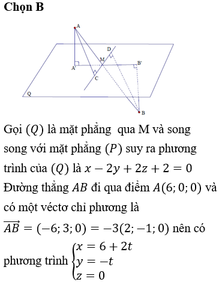





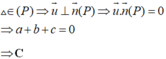
Chọn: C