Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cách 1 (Véc tơ đơn vị). Ta có
![]()
=> Tam giác OAB vuông tại O
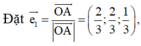
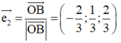

Gọi H, E là các tiếp điểm của đường tròn nội tiếp với các cạnh OA, OB.
Ta có
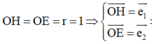
![]()
Cách 2. Kẻ phân giác OE suy ra
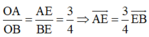
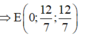
Gọi I là tâm đường tròn nội tiếp tam giác OAB
![]()
Tam giác OAB vuông tại O, có bán kính đường tròn nội tiếp r =1 ⇒ I O = 2
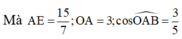
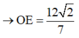
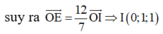

Chọn B
Cách 1:
![]()
Gọi M,N lần lượt là trung điểm AB, BC
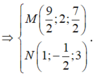
Gọi n → là véc tơ pháp tuyến của mặt phẳng (ABC).
![]()
![]()
I là tâm đường tròn ngoại tiếp tam giác ABC
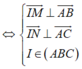
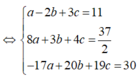
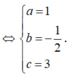
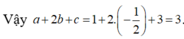
Cách 2:
Ta có
![]()
![]()
=> Tam giác ABC vuông tại B
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên I là trung điểm của AC.
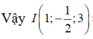
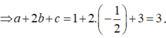
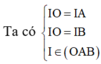
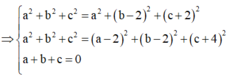
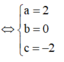
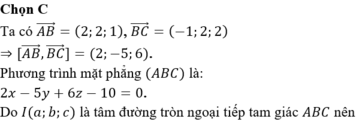
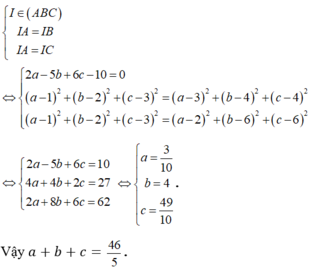

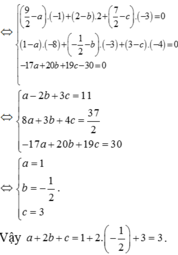


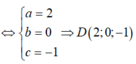

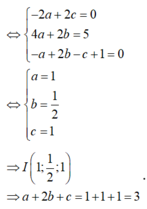
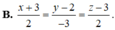
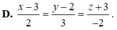

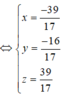



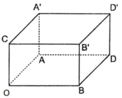



Đáp án B
Phương pháp giải:
Tâm đường tròn ngoại tiếp cách đều 3 đỉnh của tam giác và thuộc mặt phẳng chứa tam giác
Lời giải:
Vì I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC
Lại có
Kết hợp với