Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

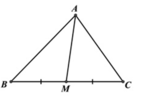
a) \(\Delta ABC\) cân tại A nên AH là đường cao đồng thời cũng là trung tuyến.
\(\Rightarrow BH=\frac{1}{2}BC=\frac{1}{2}.6=3\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại H có:
\(AH^2+BH^2=AB^2\) (Định lý Py-ta-go)
\(\Rightarrow AH^2+3^2=5^2\)
\(\Rightarrow AH^2=5^2-3^2=26-9=16\)
Mà \(AH>0\Rightarrow AH=4\left(cm\right)\)
Vậy \(BH=3\) \(cm;\) \(AH=4\) \(cm.\)
b) G là trọng tâm \(\Delta ABC\), nên G nằm trên đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow G\in AH\)
\(\Rightarrow A,G,H\) thẳng hàng.
Vậy \(A,G,H\) thẳng hàng.
c) \(\Delta ABC\) cân tại A nên AH là đường cao đồng thời là phân giác góc BAC
\(\Rightarrow AG\) là phân giác góc BAC
\(\Rightarrow\) Góc BAG = góc CAG
Xét \(\Delta BAG\) và \(\Delta CAG\), ta có:
\(AB=AC\) ( \(\Delta ABC\) cân tại A)
Góc BAG = góc CAG (Chứng minh trên)
Cạnh AG chung
\(\Rightarrow\Delta BAG=\Delta CAG\left(c.g.c\right)\)
\(\Rightarrow\) Góc ABG = góc ACG (hai góc tương ứng)
Vậy góc ABG = góc ACG.

Sửa đề; BC=12cm
a: Xét ΔABD có \(\widehat{B}=\widehat{BAD}=60^0\)
nên ΔABD đều
=>BD=AB=6cm
=>BH=3cm
b: Ta có: BD+DC=BC
nên DC=BC-BD=12-6=6(cm)
Xét ΔDAC có DA=DC
nên ΔDAC cân tại D
c: Xét ΔABC có
AD là đường trung tuyến
AD=BC/2
Do đó: ΔABC vuông tại A

Câu 1:
Sửa đề; BC=12cm
a: Xét ΔABD có \(\widehat{B}=\widehat{BAD}=60^0\)
nên ΔABD đều
=>BD=AB=6cm
=>BH=3cm
b: Ta có: BD+DC=BC
nên DC=BC-BD=12-6=6(cm)
Xét ΔDAC có DA=DC
nên ΔDAC cân tại D
c: Xét ΔABC có
AD là đường trung tuyến
AD=BC/2
Do đó: ΔABC vuông tại A