Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có ABCD là hình bình hành nên A D ⇀ = B C ⇀ = - 1 ; 3 ; 7 ⇒ D 0 ; 5 ; 10
Chọn đáp án C.

Đáp án A
Vì M ∈ d nên M t + 3 ; − t − 2 ; 2 t + 1 , t ∈ ℝ
Đường thẳng Δ có vtcp u Δ → = − 1 ; 2 ; − 3 .
Đường thẳng d ' : qua M t + 3 ; − t − 2 ; 2 t + 1 vtcp u d ' → = u Δ → = − 1 ; 2 ; − 3
⇒ d ' : x − t + 3 − 1 = y + t + 2 2 = z − 2 t + 1 − 3
M’ là hình chiếu song song của M trên (P)
⇒ M ' = d ' ∩ P ⇒ M ' 5 9 t + 2 ; − 1 9 t ; 2 3 t − 2 .
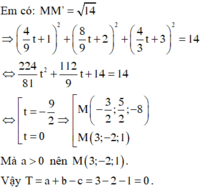

mk nghĩ đây là đề đúng
\(\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+a^2}\ge\dfrac{3}{2}\)
Ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\\\dfrac{b}{1+c^2}=b-\dfrac{bc^2}{1+c^2}\\\dfrac{c}{1+a^2}=c-\dfrac{ca^2}{1+a^2}\end{matrix}\right.\)
Áp dụng bđt AM-GM ta có:
\(\dfrac{ab^2}{1+b^2}\le\dfrac{ab^2}{2b}=\dfrac{ab}{2}\)
\(\Rightarrow a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab}{2}\) (1)
C/m tg tự ta có:
\(\left\{{}\begin{matrix}b-\dfrac{bc^2}{1+c^2}\ge b-\dfrac{bc}{2}\\c-\dfrac{ca^2}{1+a^2}\ge c-\dfrac{ac}{2}\end{matrix}\right.\) (2)
Chứng minh điều sau:\(ab+bc+ca\le3\)
Ta có:
\((a+b+c)^2\ge3(ab+bc+ca)\)
\(\Leftrightarrow9\ge3ab+3bc+3ca\)
\(\Leftrightarrow ab+bc+ca\le3\)
Từ (1) và (2)
\(\Rightarrow VT\ge a+b+c-\dfrac{ab+bc+ca}{2}\)
Mà \(ab+bc+ca\le3\)
Nên \(VT\ge a+b+c-\dfrac{ab+bc+ca}{2}\ge3-\dfrac{3}{2}=\dfrac{3}{2}\)
=> ĐPCM


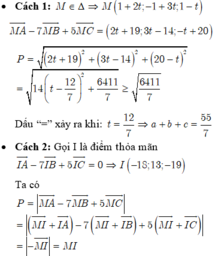
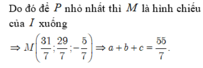
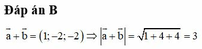
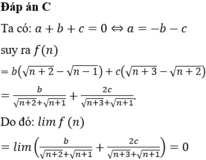
Đáp án A