Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Vecto pháp tuyến của hai mặt phẳng (P) và (Q) là :
n p → (1; -1; 2); n q → (2; -2; m2 + 3m)
Hai mặt phẳng (P) và (Q) song song với nhau khi và chỉ khi tồn tại một số thực k sao cho:
n p → = k. n q →


Đáp án A
Phương pháp : Cho hai mặt phẳng có phương trình lần lượt là :
![]()
![]()
Khi đó (P) và (Q) song song với nhau
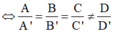
Cách giải:
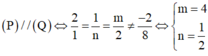

Đáp án A
Ta có:
![]()
Mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R) khi và chỉ khi
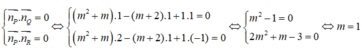

Đáp án C
Ta có: n p → = (1; m; m + 3), n Q → = (1; -1; 2).
Hai mặt phẳng (P) và (Q) vuông góc khi và chỉ khi n p → . n Q → = 0
⇔ 1.1 + m.(-1) + (m + 3).2 = 0 ⇔ m + 7 = 0 ⇔ m = -7

Chọn A
Gọi (Q) là mặt phẳng đi qua M (2;2; -3) và song song với mặt phẳng (P).
Suy ra (Q):2x+y+z-3=0.
Do Δ // (P) nên Δ ⊂ (Q)).
D (N, Δ) đạt giá trị nhỏ nhất ó Δ đi qua N', với N' là hình chiếu của N lên (Q).
Gọi d là đường thẳng đi qua N và vuông góc (P), 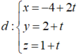
Ta có N’ ∈ d => N' (-4+2t;2+t;1+t); N’ ∈ (Q) => t = 4/3 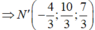
![]() cùng phương
cùng phương 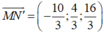
Do |a|, |b| nguyên tố cùng nhau nên chọn ![]()
Vậy |a| + |b| + |c| = 15.

Chọn A
Sử dụng tính chất: Nếu đường thẳng a vuông góc mặt phẳng (P) thì mọi mặt phẳng qua a đều vuông góc
(P) để nhận xét mối quan hệ giữa các mặt phẳng ![]()

Ta có:
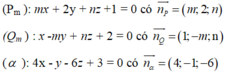
Do đó
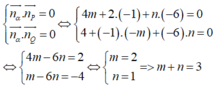



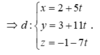

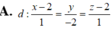
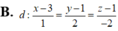
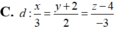

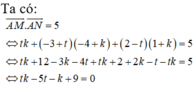

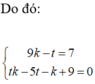
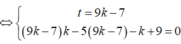
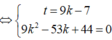
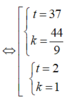

Đáp án D
Hai mặt phẳng đã cho song song khi và chỉ khi tồn tại một số thực k sao cho: