Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ


Chọn đáp án D
Phương pháp
+ Cho mặt cầu (S) có tâm I và bán kính R và mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn có bán kính r thì ta có mối liên hệ R 2 = h 2 + r 2 với h=d(I,(P)). Từ đó ta tính được R.
+ Phương trình mặt cầu tâm I ( x 0 ; y 0 ; z 0 ) và bán kính R có dạng
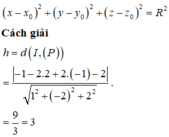
Từ đề bài ta có bán kính đường tròn giao tuyến là r=5 nên bán kính mặt cầu là
![]()
+ Phương trình mặt cầu tâm I(-1;2;-1) và bán kính R = 34 là
![]()

Đáp án A
Đường thẳng d đi qua các điểm M 3 ; 1 ; 0 và N 4 ; 2 ; 2
Xét mặt phẳng (P) có phương trình A x + B y + C z + D = 0
(P) đi qua d khi và chỉ khi (P) đi qua M và N
⇔ 3 A + B + D = 0 4 A + 2 B + 2 C + D = 0 ⇒ C = − A + B 2 D = − 3 A − B
Phương trình (P) trở thành
A x + B y − A + B 2 x − 3 A − B = 0
⇔ 2 A x + 2 B y − A + B z − 6 A − 2 B = 0
Mặt cầu (S) có tâm I − 1 ; 1 ; − 1 và bán kính R = 2 .
Giao tuyến của (P) và (S) là đường tròn có bán kính r=1. Suy ra khoảng cách từ (I) đến (P) là d = R 2 − r 2 = 4 − 1 = 3
Từ đó ta có
− 2 A + 2 B + A + B − 6 A − 2 B 4 A 2 + 4 B 2 + A + B 2 ⇔ − 7 A + B 2 = 3 5 A 2 + 5 B 2 + 2 A B
⇔ 34 A 2 − 20 A B − 14 B 2 = 0 ⇒ 34 A B 2 − 20 A B − 14 = 0 ⇒ A B = 1
hoặc A B = − 7 17
Với A B = 1 ⇒ B = A ta có phương trình (P)
2 A x + 2 A y − 2 A z − 8 A = 0 ⇔ x + y − z − 4 = 0
Với A B = − 7 17 : Chọn A = − 7, B = 17 ta có phương trình (Q): 7 x − 17 y + 5 z − 4 = 0
Gọi α là góc giữa (P) và (Q). Ta có cos α = 1.7 + 1. − 17 − 1.5 1 + 1 + 1 . 49 + 289 + 25 = 5 11 . Ta chọn đáp án A

Chọn D
Từ phương trình hai mặt phẳng (P1), (P2) cho z = 1 ta tìm được điểm A(2;2;1) thuộc mặt phẳng (α) Tìm vecto chỉ phương của đường thẳng d. Vecto pháp tuyến của mặt phẳng cần tìm là tích có hướng của vecto pháp tuyến (P) và vecto chỉ phương của d

Ta có:
![]()
lần lượt là VTPT của α ; β .
Gọi mặt phẳng cần tìm là mặt phẳng (P) có VTPT n p → .
Ta có:

Chọn C.




Đáp án D