Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}a+8-c+d=0\\\dfrac{\left|a-8+2c+d\right|}{\sqrt{a^2+16+c^2}}=5\end{matrix}\right.\)
\(\Rightarrow\left(3c-16\right)^2=25\left(a^2+c^2+16\right)\)
\(\Rightarrow25a^2+16c^2+96c+144=0\)
\(\Rightarrow25a^2+16\left(c+3\right)^2=0\Rightarrow\left\{{}\begin{matrix}a=0\\c=-3\end{matrix}\right.\)
\(\Rightarrow d=c-a-8=-11\)
\(\Rightarrow a+c+d=-14\)

Chọn D
Gọi I là trung điểm của AB, suy ra I (1;1;1); ![]()
Phương trình mặt phẳng trung trực của AB: (α): 2x + y -3 = 0.
Vì (2.3 + 1.2 - 3). (2.5 + 1.3 - 3) = 50 > 0 nên B, C nằm về một phía so với (α), suy ra A, C nằm về hai phía so với (α).
Điểm M thỏa mãn MA = MB khi M ∈ (α).
Khi đó MB + MC = MA + MC ≥ AC.
MB + MC nhỏ nhất bằng AC khi M = AC ∩ (α)
Phương trình đường thẳng AC: 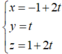
do đó tọa độ điểm M là nghiệm của hệ phương trình
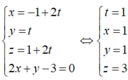
Do đó M (1; 1; 3), a + b + c = 5

\(\overrightarrow{AB}=\left(8;0;-2\right)=2\left(4;0;-1\right)\)
Phương trình AB có dạng: \(\left\{{}\begin{matrix}x=5+4t\\y=2\\z=2-t\end{matrix}\right.\)
Tọa độ M thỏa mãn:
\(5+4t+2-3\left(2-t\right)+4=0\) \(\Rightarrow t=-\dfrac{5}{7}\)
\(\Rightarrow M\left(\dfrac{15}{7};2;\dfrac{19}{7}\right)\) \(\Rightarrow\left\{{}\begin{matrix}MA=\dfrac{9\sqrt{17}}{7}\\MB=\dfrac{5\sqrt{17}}{7}\end{matrix}\right.\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{9}{5}\)

Chọn C
![]()
Suy ra ABCD là hình bình hành.
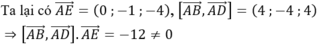
=>E.ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.

Chọn B
Ta có AB=3, AC=6. Gọi I (x; y; z) là điểm thuộc cạnh BC sao cho AI là phân giác trong của góc A

Phương trình mặt phẳng (Oxy) là: z=0.
Giao điểm của đường thẳng AI với mặt phẳng (Oxy) là M (2; 7/3; 0)
Vậy 3b-a=5.
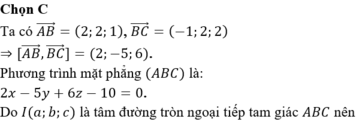
Đáp án A.