Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp:
Từ các giả thiết đã cho, lập hệ 3 phương trình ba ẩn a, b, c. Giải hệ phương trình tìm a, b, c và tính tổng S.
Cách giải:
![]()
![]()
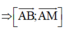
![]()
![]()
⇒ 2 ( 16 b + 4 c - 40 ) - ( - 16 a + 2 c - 12 ) + ( - 4 a - 2 b + 2 ) = 0
Ta có
![]()
M A 2 + M B 2 = 246
⇒ a + 1 2 + b - 3 2 + c + 2 2 + ( a + 3 ) 2 + ( b - 7 ) 2 + ( c + 18 ) 2 = 246
![]()
Khi đó ta có hệ phương trình
![]()
![]()
Thay vào (3) ta có
a 2 + 4 + ( 1 - 2 a ) 2 + 4 a - 10 . 2 + 20 ( 1 - 2 a ) + 75 = 0
![]()
![]()
![]()

Gọi G là trọng tâm tam giác ABC \(\Rightarrow G\left(2;1;0\right)\)
\(T=MA^2+MB^2+MC^2\)
\(T=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(T=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(T=3MG^2+GA^2+GB^2+GC^2\)
Do \(GA^2+GB^2+GC^2\) cố định nên \(T_{min}\) khi \(MG_{min}\)
\(\Rightarrow M\) là hình chiếu vuông góc của G lên (P)
Gọi (d) là đường thẳng qua G và vuông góc (P) \(\Rightarrow\) pt (d): \(\left\{{}\begin{matrix}x=2+t\\y=1+t\\z=t\end{matrix}\right.\)
M là giao điểm (d) và (P) nên thỏa mãn:
\(2+t+1+t+t=0\Leftrightarrow t=-1\) \(\Rightarrow M\left(1;0;-1\right)\)

Đáp án D
Phương trình mặt phẳng trung trực của AB là
![]()
Phương trình mặt phẳng trung trực của AC là
![]()
Chọn x = 1
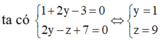
![]()
Phương trình đường thẳng giao tuyến của ( α ) và ( β ) là
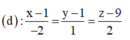
Vì MA=MB=MC
![]()
![]()
![]()
![]()
![]()

a. Mặt phẳng (P) có (3;-2;2) là 1 vtpt nên d nhận (3;-2;2) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+3t\\y=2-2t\\z=-1+2t\end{matrix}\right.\)
b. \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) ; \(\overrightarrow{n_{\left(P'\right)}}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(P'\right)}}\right]=\left(2;0;-2\right)=2\left(1;0;-1\right)\)
\(\Rightarrow\) d nhận (1;0;-1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=-2\\z=3-t\end{matrix}\right.\)
c. \(\overrightarrow{u_{\Delta}}=\left(3;2;1\right)\) ; \(\overrightarrow{u_{\Delta'}}=\left(1;3;-2\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{u_{\Delta'}}\right]=\left(-7;7;7\right)=7\left(-1;1;1\right)\)
Đường thẳng d nhận (-1;1;1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=-1-t\\y=1+t\\z=3+t\end{matrix}\right.\)

Chọn A
Thay tọa độ hai điểm A (3;1;0), B (-9;4;9) vào vế trái phương trình mặt phẳng (P), ta có
2. 3-1+0+1=6 > 0 và 2. (-9)-4+9+1 = -12 < 0.
Nên suy ra, hai điểm A, B nằm khác phía với mặt phẳng (P).
Gọi A' (-1;3;-2) là điểm đối xứng với điểm A qua mặt phẳng (P). Ta có
![]()
Dấu “=” xảy ra khi và chỉ khi A', B, I thẳng hàng và I nằm ngoài đoạn A'B. Suy ra I là giao điểm của đường thẳng A'B và mặt phẳng (P).
Ta có ![]() , nên suy ra phương trình đường thẳng A'B là
, nên suy ra phương trình đường thẳng A'B là 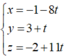 .
.
Tọa độ điểm I là nghiệm của hệ phương trình
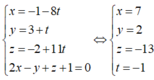
Vậy I (7;2;13) nên a+b+c=7+2+ (-13)=-4.

Chọn B
Ta có A, B cùng nằm về một phía của (P). Gọi A' đối xứng với A qua (P) suy ra A' (-2; 2; 1). Ta có MA + MB = MA' + MB ≥ BA'. Dấu bằng xảy ra khi M là giao điểm của BA' và (P). Xác định được 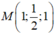 . Suy ra Chọn B
. Suy ra Chọn B
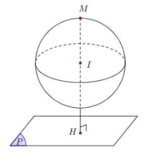

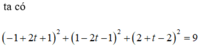
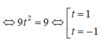
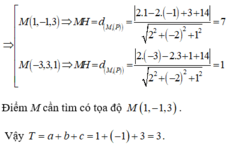
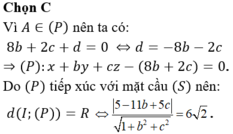
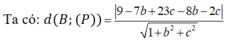
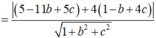
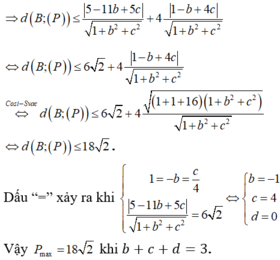
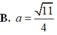
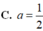

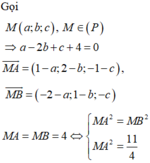
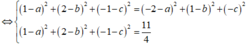

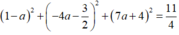
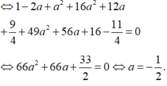
Đáp án D.