Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
C18 , c19 là lm sao vậy ạ ? Mk ko hiểu 2 bài này nơi

Số hạng tổng quát:
\(C_{18}^kx^{3k}x^{-3\left(18-k\right)}=C_{18}^kx^{6k-54}\)
Số hạng ko chứa x \(\Rightarrow6k-54=0\Rightarrow k=9\)
Số hạng đó là \(C_{18}^9=...\)

Chọn D
Số hạng tổng quát trong khai triển ( 2 x - 1 ) 2019 là
![]()
![]()
![]()
Theo đề bài ta có: 2019 - k = 18 => k = 2001.
Vậy trong khai triển biểu thức đã cho, số hạng chứa x 18 là:
![]()
![]()

\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{ax^2+bx}-cx\right)=\lim\limits_{x\rightarrow+\infty}\frac{\left(a-c^2\right)x^2+bx}{\sqrt{ax^2+bx}+cx}=\lim\limits_{x\rightarrow+\infty}\frac{\left(a-c^2\right)x+b}{\sqrt{a+\frac{b}{x}}+c}\)
Để giới hạn đã cho là hữu hạn bằng -2
\(\Leftrightarrow\left\{{}\begin{matrix}c^2+a=18\\a-c^2=0\\\frac{b}{\sqrt{a}+c}=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=9\\c^2=9\\\frac{b}{3+c}=-2\end{matrix}\right.\) \(\left(c\ne-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a=9\\c=3\\c=-12\end{matrix}\right.\) \(\Rightarrow P=12\)

Chọn B
Ta có: ( 2 x - 1 ) 2019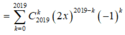
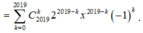
Số hạng tổng quát của khai triển là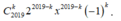 .
.
Để có x 18 thì 2019 - k = 18 => k = 2001.
Khi đó số hạng chứa x 18 là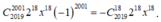 .
.