Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử hội trường có a dãy và b là số ghế của mỗi dãy. (a,b∈N∗a,b∈N∗).
Ta có phương trình: ab=500ab=500 và
⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25
Vậy lúc đầu người ta định xếp 2525 dãy ghế.

gọi dãy ghế lúc đầu là x (đk : x>0, x thuộc Z) thì số dãy ghế sau khi xếp lại là x+5
theo đề bài, ta có :
số ghế mỗi dãy lúc đầu là 120/x
số ghế mỗi dãy sau khi xếp lại là (120/x)-4 / x+5 = 120-4x / x(x+5)
ta có phương trình : 120/x - 4 = 120-4x / x(x+5)
<=> 120-4x / x = 120-4x / x(x+5)
<=> (120-4x)(x+5) / x(x+5) = 120-4x / x(x+5)
<=> (120-4x)(x+5)=120-4x
<=> (120-4x)(x+5) - (120-4x) = 0
<=> (120-4x)(x+5-1) = 0
<=> (120-4x)(x+4) = 0
<=> 120-4x = 0
x+4 =0
<=> x = 30 (thỏa đk)
x = -4 (ko thỏa đk)
vậy số dãy ghế ban đầu là 30

Chẳng phải đề bài cho số ghế có trong hội trường là 208 ghế rồi sao?

gọi số hàng ghế là x
theo đề ta có\(\left(\frac{300}{x}+2\right)\left(x-3\right)=289\Leftrightarrow-\frac{900}{x}+2x+5=0\\ \Leftrightarrow2x^2+5x-900=0\)
\(\Leftrightarrow\left(x-20\right)\left(2x+45\right)=0\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-\frac{45}{20}\left(lộai\right)\end{cases}}\)
vậy có 20 hàng ghế

Đáp án : Hội trường có 10 dãy ghế hoặc 20 dãy ghế, giải thích các bước giải :
Gọi số ghế ban đầu là x, x thuộc N* => ban đầu mỗi dãy ghế có 200/x ghế
=> Vì phải kê thêm 2 dãy ghế => Ta có x + 2 dãy ghế
=> Vì mỗi dãy phải ngồi thêm 2 người => mỗi dãy lại có : 200/x + 2 ghế
=> Số người đc ngồi là : ( x + 2 ) . ( 200/x + 2 ). Vì có 6 người k có ghế nên ( x + 2). ( 200/x + 2 ) +6= 270
=> ( x +2). ( 200/x + 2) = 264
=> ( x +2). ( 200 +2x ) = 264x
=> 2x2 + 400 + 204x = 264x
=> 2x2 - 60x + 4000 = 0
=> 2(x-10 ). ( x -20 ) = 0, Kết luận vậy từ đây ta có thể suy ra đc x thuộc { 10; 20 }

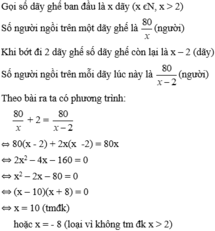
Vậy số dãy ghế ban đầu là 10 dãy và số người ngồi trên 1 dãy là 8 người.